
Passo 1
letra a)
Ser normalizada significa que:
Substituindo a função de onda temos:
Passo 2
letra b)
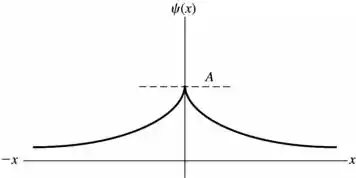
Passo 3
letra c)
A probabilidade de encontrar a partícula numa dada posição é:
Passo 4
i) Até da origem:
Passo 5
ii) Ao lado da origem:
Passo 6
iii) De até
Resposta
letra a)
letra b)
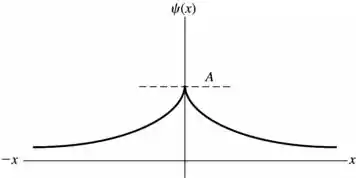
letra c)i) ; ii) ; iii)