Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 56

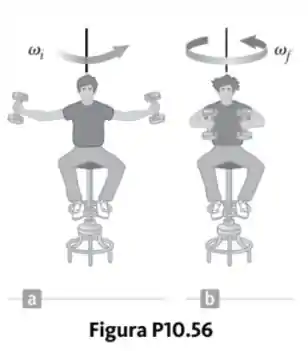
Um aluno senta-se em um banquinho, girando livremente, segurando dois halteres, cada um de massa 3,00   k g (Fig. P10.56). Quando seus braços estão estendidos horizontalmente (Fig. P10.56a), os halteres estão a 1,00   m do eixo de rotação, e o aluno gira com uma velocidade angular de 0,750   r a d / s . O momento de inércia do aluno mais o banquinho é de 3,00   k g ⋅   m 2 e supõe-se ser constante. O aluno puxa os halteres para dentro horizontalmente até uma posição 0,300   m do eixo de rotação (Fig.P10.56b).

  1. Encontre a nova velocidade angular do aluno.
  2. Encontre a energia cinética do sistema em rotação antes e depois de ele puxar os halteres para dentro.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

O momento angular total do sistema sobre o eixo de rotação são dados por:

I total  = I pesos   + I aluno   = 2 m r 2 + 3.00 k g ⋅ m 2

Antes temos r = 1.00 m , então:

I i = 2 ( 3.00 k g ) ( 1.00 m ) 2 + 3.00 k g ⋅ m 2 = 9.00 k g ⋅ m 2

Depois temos r = 0.300 m , então:

I f = 2 ( 3.00 k g ) ( 0.300 m ) 2 + 3.00 k g ⋅ m 2 = 3.54 k g ⋅ m 2

Agora usamos a conservação do momento angular:

I f ω f = I i ω i

ω f = I i I f ω i = 9.00 3.54 0.750 r a d s = 1.91 r a d s

Passo 2

Letra b:

K i = 1 2 I i ω i 2 = 1 2 9.00 k g ⋅ m 2 ( 0.750 r a d / s ) 2 = 2.53 J K f = 1 2 I f ω f 2 = 1 2 3.54 k g ⋅ m 2 ( 1.91 r a d / s ) 2 = 6.44 J

Resposta

  1. 1.91 r a d s
  2. 2.53 J   e   6.44 J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pista é montada em uma grande roda que pode girar livremente, com atrito desprezível, em torno de um eixo vertical (figura abaixo). Um trem de brinquedo de massa m é colocado na pista e, com o sis
Uma barata está no centro de um disco circular que gira livremente como um carrossel, sem torques externos. A barata caminha em direção à borda do disco, cujo raio é R . A figura abaixo mostra a veloc
Uma barata de massa 0,17 k g corre no sentido anti-horário na boda de um disco circular de raio 15 c m e momento de inércia 5.10 - 3 k g . m ² ², montado em um eixo vertical com atrito desprezível. A
O momento de inércia de uma estrela sofre uma contração enquanto gira em torno de si mesma cai para 1 / 3 do valor inicial. Qual é a razão entre a nova energia cinética de rotação e a energia antiga?
Um homem está em pé em uma plataforma que gira (sem atrito) com uma velocidade angular de 1,2 r e v / s ; seus braços estão abertos e ele segura um tijolo em cada mão. O momento de inércia do sistema