Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 11.Problemas - Ex. 51
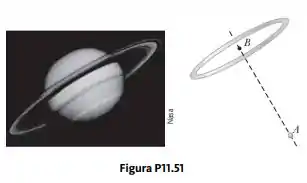
Um anel de matéria é uma estrutura familiar na astronomia planetária e estelar. Exemplos são os anéis de Saturno e a Nebulosa do Anel. Considere um anel de massa uniforme e raio de . Um corpo de massa de é colocado em um ponto no eixo do anel, a do centro deste (Fig. P). Quando o corpo é liberado, a atração do anel faz que ele se mova ao longo do eixo em direção ao centro do anel (ponto ). Calcule a energia potencial gravitacional do sistema anel-corpo quando o corpo está em . Calcule a energia potencial gravitacional do sistema quando o corpo está em . Calcule a velocidade do corpo quando ele passa por .
Passo 1
Vamos juntos detonar com essa questão!
A energia potencial gravitacional é dada por:
Onde é a distância entre os corpos, tanto no item quanto no item vamos usar essa equação para encontrar oque eles querem, o que vai mudar para cada caso é o .
No item para achar a velocidade em vamos usar a conservação de energia ao nosso favo, onde inicialmente no ponto só temos energia potencial gravitacional e no ponto temos energia cinética (de onde vamos tirar a velocidade) e energia potencial gravitacional.
Vamos as contas!
Passo 2
Começando com o item .
Para podermos calcular a energia potencial no ponto temos que saber a distância entre o anel e o corpo, e para isso podemos usar Pitágoras ao nosso favor, assim:
Então temos que:
Assim temos que:
Passo 3
Agora para o item .
Nesse caso a distância vai ser igual ao raio do anel, assim:
Assim temos que:
Passo 4
Agora para o item .
Da conservação de energia que falamos no passo , temos:
Substituindo com o que temos, ficamos com:
Então temos que:
Prontinho! Encontramos tudo que ele queria.