Exercícios de Conservação de Energia - Lista de Exercícios Resolvida
Questão 1
Um corpo é lançado diretamente para cima da superfície da Tera, com uma rapidez inicial de . Qual é a altura máxima que ele alcança?
Dados:
Ver solução completaQuestão 2
Um corpo é largado, a partir do repouso, de uma altura de acima da superfície da Terra. Se não existe resistência do ar, qual é sua rapidez ao atingir a Terra?
Dados:
Ver solução completaQuestão 3
O gráfico abaixo representa a aceleração da gravidade (em ) em função da distância ao centro de um asteroide esférico cujo raio é de
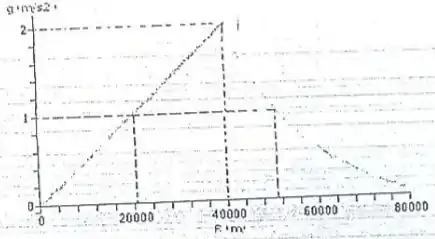
(a) Calcule a velocidade de escape de um corpo neste asteroide.
(b) Até que distância da superfície irá o corpo se ele deixar a superfície do asteroide com uma velocidade radial de ?
Ver solução completaQuestão 4
Uma pedra de massa caindo em queda livre é capturada por uma pessoa de inércia . Ao atingir a mão da pessoa a pedra tem velocidade , e durante a captura o braço da pessoa se desloca verticalmente para baixo por uma distância . Considerando um sistema formado pela pedra+planeta, calcule o trabalho realizado por cada força externa que age no sistema entre o instante que a pessoa inicia o movimento de captura da pedra até o instante que a pedra para na mão da pessoa. Escreva a Lei de conservação de Energia do sistema pedra+planeta.
Ver solução completaQuestão 5
Um corpo de massa é lançado da superfície da Terra. Seja a massa da Terra e o raio da Terra. Despreze a resistência do ar.
a) Qual a velocidade mínima requerida para mandar o projétil a uma altura de acima da superfície da Terra? Dê sua resposta em função de , e , onde é a constante gravitacional.
b) Considere agora a situação onde o projétil se mantém em órbita circular em torno da Terra a uma altura de acima da superfície. Calcule o módulo da velocidade do projétil. Dê sua resposta em função de , e .
c) Agora, calcule o módulo da velocidade de lançamento(a partir da superfície) necessária para que o projétil se mantenha em órbita circular a uma altura de acima da superfície terrestre. Dê sua resposta em função de , e .
Ver solução completaQuestão 6
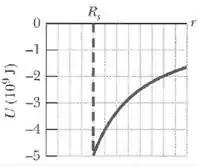
A figura mostra a energia potencial de um projétil em função da distância da superfície de um planeta de raio . Se o projétil é lançado verticalmente para cima com uma energia mecânica de , quais são sua energia cinética a uma distância e seu ponto de retorno em termos de ?
Questão 7
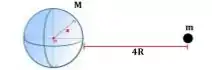
Uma partícula pontual de massa está a uma distância da superfície de uma esfera de massa e raio , conforme ilustrado na figura abaixo. Se mantivermos a esfera fixa e soltarmos a partícula do repouso, deixando que a força gravitacional desloque a partícula em direção à esfera, com que velocidade a partícula atingirá a superfície da esfera? Nas respostas abaixo, significa a constante universal da gravitação.
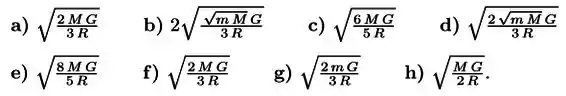
Questão 8
Um pequeno satélite descreve um movimento circular uniforme em torno de um planeta esférico, sob a ação da força gravitacional. A massa específica do planeta é uniforme. Indique a(s) alternativa(s) correta(s): No referencial do planeta, a energia mecânica é , onde:
Ver solução completa
Questão 9
Uma partícula é lançada verticalmente a partir da superfície da Terra com velocidade de módulo . Ela atinge uma altura máxima em relação ao solo. Desprezando efeitos de atrito, determine .
Suponha um planeta de massa m segue uma órbita circular de raio e período ao redor de uma estrela de massa . Denotando por a constante gravitacional de Newton, calcule uma expressão para a razão em termos de e .
Considere um anel de raio e massa total cujo centro está a uma distância de uma partícula pontual de massa , conforme ilustrado na figura abaixo. Calcule a força gravitacional que age na partícula de massa , incluindo sua direção e sentido.
[Dica: Particione o anel em pequenos pedaços de massa infinitesimal e use argumentos de simetria para justificar que apenas uma componente da força é diferente de zero. Outra maneira de fazer o problema é calcular a energia potencial de interação e depois tomar a derivada em relação a .]
Dados:
Ver solução completaQuestão 10
1. Um veículo possui massa de tonelada e quatro rodas de liga leve de massa cada e diâmetro de . Outro veículo idêntico possui rodas de aço de de diâmetro, e mesma massa das de liga leve. Compare a velocidade dos veículos ao final de uma descida de de comprimento e inclinação de . Suponha que ambos os veículos tenham velocidade inicial nula.
Ver solução completaQuestão 11
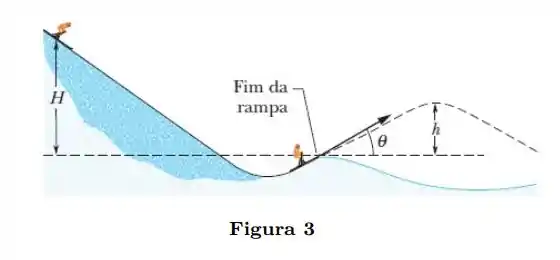
Um esquiador de parte do repouso a uma altura acima da extremidade de uma rampa para saltos de esqui (Fig. 3), e deixa a rampa fazendo um ângulo de com a horizontal. Despreza os efeitos da resistência do ar e suponha que a rampa não tem atrito. Qual é a altura máxima do salto em relação a extremidade da rampa? Se o esquiador aumentasse o próprio peso colocando uma mochila nas costas, seria maior, menor ou igual?
Questão 12
Um objeto de sofre a ação de uma força conservativa dada por , com em newtons e em metros. Tome a energia potencial associada a essa força como sendo nula quando o objeto está em . Qual é a energia potencial associada a essa força quando o objeto está em ? se o objeto possui uma velocidade de no sentido negativo do eixo quando está em , qual é a sua velocidade ao passar pela origem? Quais são as respostas dos itens e se a energia potencial do sistema é tomada como sendo quando objeto está em ?
Ver solução completaQuestão 13
Consideramos um satélite de em uma órbita aproximadamente circular acima da superfície da Terra. Suponha que o satélite perde energia mecânica a uma taxa média de por revolução orbital. Considerando o raio da Terra , a massa da Terra e .
- Quais são a velocidade e o período do satélite na órbita inicial?
- Calcule a energia mecânica do satélite na órbita inicial
- Usando a aproximação que a órbita do satélite se torna uma circunferência cujo raio diminui lentamente, determine a altitude e a velocidade ao final da revolução número
- Determine o módulo da força restauradora média que a atua sobre o satélite.
Questão 14
Um satélite artificial da Terra passa de uma órbita circular de raio para um órbita circular de raio . Durante a transição,
(a) A força gravitacional realiza um trabalho negativo, a energia cinética do satélite diminui e a energia potencial do sistema Terra-satélite aumenta
(b) a força gravitacional realiza um trabalho positivo, a energia cinética do satélite aumenta e a energia potencial do sistema Terra-satélite aumenta
(c) a força gravitacional realiza um trabalho positivo, a energia cinética do satélite aumenta e a energia potencial do sistema Terra-satélite diminui
(d) a força gravitacional realiza um trabalho positivo, a energia cinética do satélite diminui a energia potencial do sistema Terra-satélite aumenta
(e) a força gravitacional realiza um trabalho negativo, a energia cinética do satélite aumenta e a energia potencial do sistema Terra-satélite diminui
Ver solução completaQuestão 15
Para medir a massa de um planeta cujo raio é cinco vezes o raio da Terra, um astronauta deixa cair um objeto, a partir do repouso, a uma altura de 30 metros acima da superfície do planeta. Quando o objeto chega à superfície do planeta, sua velocidade é o dobro da velocidade que o objeto teria caso o mesmo experimento tivesse sido realizado na Terra. Qual é a massa desse planeta?
Ver solução completaQuestão 16
A figura abaixo ilustra um satélite de massa que está em movimento em uma órbita elíptica ao redor de um planeta de massa . O planeta encontra-se localizado em um dos focos da elipse (ponto ). As distâncias mínima e máxima entre o planeta e o satélite são, respectivamente, (distância entre o foco e o ponto , chamado periélio) e (distância entre o foco e o ponto , chamado afélio). Nestas condições:
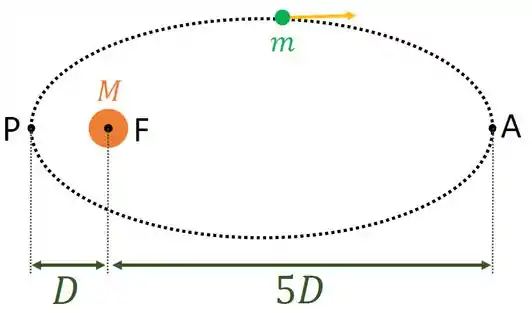
(a) Determine a razão entre a energia mecânica do sistema no ponto e a energia mecânica no ponto , isto é, .
(b) Calcule o módulo das velocidades do satélite nos pontos e .
Ver solução completa