Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.4 - Ex. 39
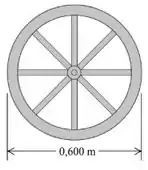
9.39 Uma roda de carroça é feita como indicado na Figura . O raio da roda é igual a m e o aro possui massa igual a . Cada um dos seus oito raios, distribuídos ao longo de diâmetros, possuem comprimento de m e massa igual a . Qual é o momento de inércia da roda em relação a um eixo perpendicular ao plano da roda e passando pelo seu centro? (Use as fórmulas indicadas na Tabela .)
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o momento de inércia da roda em relação a um eixo perpendicular ao plano da roda e passando pelo seu centro.
A principio podemos observar que cada um dos oito raios da roda podem ser considerados uma barra delgada de mesma massa e comprimento com o eixo passando por uma extremidade de cada. Sendo assim, o momento de inercia dessas barras será dado por:
O momento de inercia do aro de massa e raio por tabela, será:
Agora fica facinho de calcular o momento de incercia do sistema (que será o da roda), pois sabemos que é só somar o momento de incerica de cada um dos corpos que teremos o do sistema.
Vamos lá!
Passo 2
Sendo assim, vemos que o momento de inercia do sistema é:
Substituindo os valores fornecidos no enunciado, teremos:
Portanto,
Valeu, galera! Até a próxima! 😉