Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 9.Problemas - Ex. 58
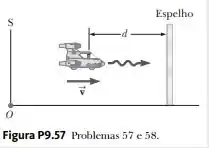
. Um observador em uma espaçonave de cruzeiro move-se em direção a um espelho a uma velocidade relativa ao referencial da Figura P9.57. O espelho está parado em relação a . Um pulso de luz é emitido por uma espaçonave que viaja em direção ao espelho e é refletido de volta à espaçonave. A espaçonave está a uma distância do espelho (conforme medida pelos observadores em ) no momento em que o pulso de luz deixa a espaçonave. Qual é o tempo total de viagem do pulso conforme medido pelos observadores no referencial e na espaçonave?
Passo 1
O tempo próprio é o intervalo de tempo entre dois eventos que acontecem no mesmo lugar, ou seja, a primeira coisa que temos que fazer quando pegamos um exercício assim é identificar o referencial no qual pertence o tempo próprio, então vamos analisar.
No referencial o observador ver um pulso saindo da nave em um instante enquanto a nave está em uma posição e ver o pulso voltando em um instante quando a nave se moveu até uma posição .
Por outro lado, no referencial da nave ela libera o pulso no instante na posição e recebe o pulso no instante na posição , isto é, para a nave (no referencial dela) ela não mudou de posição, então os dois eventos de emitir o pulso e receber o pulso aconteceram na mesma posição o que significa que o tempo próprio é o intervalo de tempo dos dois eventos visto da nave.
Essa é uma das ideias mais importantes nesse tipo de exercício e agora que esclarecemos vamos começar a resolver a questão.
Passo 2
O observador em ver o pulso que a nave emitiu percorrer uma distância até o espelho e, após o pulso refletir no espelho, viu ele voltar para a nave percorrendo um caminho .
Mas porque tem esse termo ? Vamos lembrar que a nave está em movimento então a nova posição que ela estará quando o pulso chegar nela vai depender da sua velocidade e do tempo que demorou pra ele voltar.
Sendo assim temos que a distância total percorrida pelo pulso foi:
Sabendo que:
Isolando o temos:
Passo 3
Esse item está nos pedindo o tempo próprio e pela equação sabemos que:
é o que conseguimos no item anterior então vamos achar o .
Sendo assim o resultado desse item é dado por:
Resposta