Um sinal luminoso que, partindo de um ponto de um referencial (), se reflete num espelho à distância de e volta para, pode ser considerado como um relógio que marca intervalos de tempo correspondentes à ida e volta do sinal (fig.). Suponha que () se desloca em relação a () com velocidade na direção de e calcule o intervalo de tempo correspondente em (), admitindo o princípio da constância da luz. Mostre que o resultado equivale à dilatação dos intervalos de tempo da relatividade restrita.
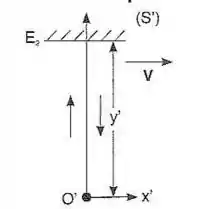
Passo 1
Cada observador verá a seguinte trajetória do sinal luminoso:
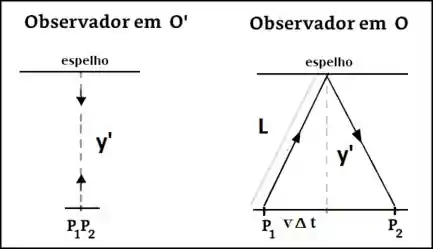
Passo 2
Para o observador em , o sinal luminoso viaja em uma linha reta. O intervalo de tempo do sinal luminoso é dado por:
Contudo, para um observador em , o sinal percorre a trajetória mostrada no desenho e o intervalo de tempo será:
Passo 3
Pelo desenho podemos e usando Pitágoras.
Passo 4
Substituindo teremos:
Passo 5
Como sabemos o intervalo de tempo no referencial , podemos relacionar:
que é a dilatação temporal.