Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 2.Problemas - Ex. 13
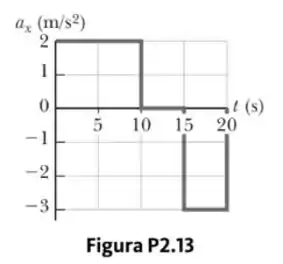
Uma partícula começa do repouso e acelera como demonstrado na Figura P2.13. Determine
- a velocidade da partícula em t = 10,0 s e em t = 20,0 s, e
- a distância percorrida nos primeiros 20,0 s.
Passo 1
E aí, pessoal, bora mais uma?
Aqui não tem muito mistério, você só precisa saber que em gráficos do tipo , a área entre a curva do gráfico e o eixo equivale à velocidade do corpo no instante delimitado!
Então se a gente calcular a área do retângulo formado entre a curva e o eixo no ponto , vamos determinar a velocidade do corpo nesse instante.
Vamos ter o seguinte:
a.
Onde e são a base e a altura do retângulo delimitado por . Olhando os valores de e no gráfico, a gente responde facinho. Teremos:
Passo 2
b.Agora queremos a distância percorrida em 20 segundos, ou seja, do percurso inteiro!
Pra isso, a gente vai precisar saber as velocidades praticadas pela partícula pelas áreas delimitadas entre a curva e o eixo horizontal. A primeira a gente já calculou no Passo 1, vamos calcular a outra, que é a área do retângulo com vértices em e .
Vamos ter:
Essa velocidade negativa indica que a partícula começou a voltar pra trás no percurso que seguia a partir do instante , que é onde ela começa a desacelerar (ou acelerar pra trás).
Passo 3
Agora, com as velocidades ao longo do percurso calculadas, a gente consegue determinar a velocidade média do percurso, que nada mais é que a média dessas velocidades. Temos:
Em outras palavras, é como se a partícula tivesse alcançado seu destino com essa velocidade durante todo o trajeto! Não foi assim na prática, mas matematicamente seria equivalente a isso, sacou?
Passo 4
Bom, temos a velocidade média do percurso todo, de , e o tempo que a partícula levou pra executá-lo, de .
Com esses dados a gente consegue obter o tamanho do percurso, a distância , uma vez que:
Teremos, nos primeiros 10s:
Entre 10 e 15s: a velocidade é constante, já que a=0. Logo:
Entre 15 e 20s:
Somando as 3 distâncias, teremos:
Resposta
a.
b.