A Figura P2.15 mostra um gráfico de versus para o movimento de um motociclista que começa do repouso e se move ao longo da estrada em uma linha reta.
- Encontre a aceleração média para o intervalo de tempo t = 0 a t = 6,00 s.
- Calcule o instante em que a aceleração tem seu maior valor positivo e o valor da aceleração nesse instante.
- Quando a aceleração é zero?
- Calcule o valor negativo máximo da aceleração e o instante em que ocorre.
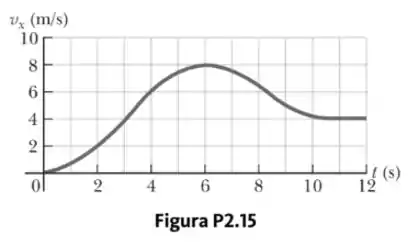
Passo 1
Bora mais uma? Vai ser tranquila!
a.A aceleração média tem a seguinte formulinha:
Ou seja, a razão entre a variação da velocidade em dois instantes diferentes e o intervalo de tempo entre esses instantes.
O é facinho, que é , agora vamos determinar pelo gráfico, olhando os valores respectivos de correspondentes a e .
Vamos ter:
Com isso, então, a gente tem:
Passo 2
b.Como a gente sabe, a aceleração é a derivada da velocidade. Se a gente não tem a equação dessa curva pra derivar, vai no olho mesmo!
A derivada de maior valor positivo vai passar pelo ponto em que a reta tangente é a mais inclinada possível, a que mais tende à vertical.
Se você olhar bem, no gráfico, isso vai acontecer no ponto , mais ou menos, que é perto do ponto de inflexão da curva!
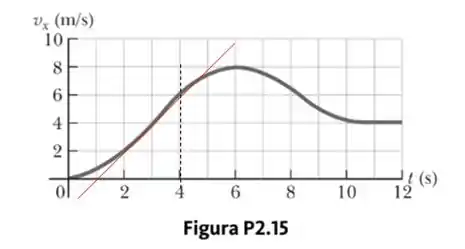
E pra saber o valor da aceleração nesse ponto? É só a gente determinar . Repara que a reta vermelha faz um triângulo retângulo. Nesse triângulo a gente determina essa relação.
Temos:
Assim, esse é o maior valor de aceleração:
Passo 3
c.A aceleração vai ser nula nos pontos de máximo/mínimo ou regiões do gráfico em que a curva é constante (paralela ao eixo ).
Pelo gráfico, dá pra gente notar que esses instantes de aceleração zero acontecem em e, de novo, a partir de .
Passo 4
d.Aqui é igual ao Passo 2, mas vamos avaliar a aceleração negativa de maior módulo, ou seja, quando o gráfico estiver decrescente.
Isso vai acontecer mais ou menos em
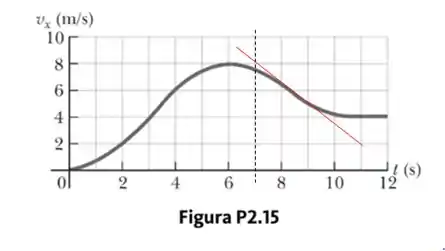
Temos:
Logo !
Resposta
a.
b.
c. Em e a partir de
d.