Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 70

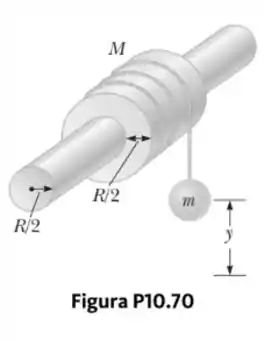
Uma bobina oca, cilíndrica e uniforme tem raio interno R / 2 , raio externo R e massa M (Fig. P10.70). Ela é montada de modo a girar em um eixo horizontal fixo. Um contrapeso de massa   m é conectado à ponta de um cordão enrolado ao redor da bobina. O contrapeso cai do repouso em t   =   0 para uma posição y no instante t . Mostre que o torque devido às forças de atrito entre bobina e eixo é

T f = R m g - 2 y t 2 - M 5 y 4 t 2

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

τ f irá se opor ao torque devido ao objeto pendurado:

∑ τ = I α = T R - τ f

τ f = T R - I α                         1

Agora encontre T , I ,   e  α em termos dados ou conhecidos e substitua na equação [1]:

∑ F y = T - m g = - m a

T = m g - a                         2

Passo 2

Também temos que:

Δ y = v i t + a t 2 2 a = 2 y t 2                               3

E

α = a R = 2 y R t 2                           4

I = 1 2 M R 2 + R 2 2 = 5 8 M R 2                     5

Substituindo [2], [3], [4] e [5] em [1], encontramos:

τ f = m g - 2 y t 2 R - 5 8 M R 2 2 y R t 2 = R m g - 2 y t 2 - 5 4 M y t 2

Resposta

R m g - 2 y t 2 - 5 4 M y t 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pêndulo consistindo em um fio de comprimento L preso a uma bolinha de massam oscila em um plano vertical. Quando o fio forma um ângulo θ com a vertical, (a) calcule a aceleração tangencial da bolin
Um cilindro de 2,5 k g , cujo raio é de 11 c m , inicialmente em repouso, pode girar livremente em torno de seu eixo. Uma corda de massa desprezível é enrolada em torno dele e puxada com uma força de
Um disco horizontal uniforme, de massa M e raioR , gira em torno do eixo vertical que passa pelo seu centro de massa com uma rapidez angular ω . Quando o disco, girando, é largado sobre uma mesa horiz
Um bloco de 2000 k g é levantado, com rapidez constante de8,0c m / s , por um cabo de aço ligado por uma polia a um guincho motorizado. O raio do tambor do guincho é 30 c m . (a) Qual é a tensão no ca
Você amarra um fio fino a um ponto na periferia de um disco uniforme vertical de raio R e massa M. O disco pode girar livremente sem atrito em um eixo horizontal fixo que passa peloseu centro de massa