Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 6.Problemas - Ex. 50
Um sistema consiste em três partículas, cada uma de massa 5,00 g, localizadas nos vértices de um triângulo equilátero com lados de 30,0 cm.
a.Calcule a energia potencial que descreve as interações gravitacionais internas ao sistema.
b.Se as partículas são liberadas simultaneamente, onde elas irão colidir?
Passo 1
Vamos começar esboçando mais ou menos a situação:
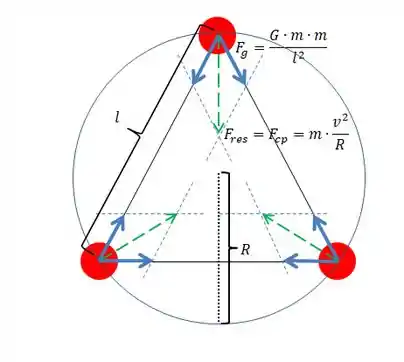
Aqui é importante a gente entender, em primeiro lugar, como agem as forças de atração gravitacional no sistema, com toda a simetria, e as forças resultantes também.
Nesse caso a gente não vai precisar calcular essas forças, mas vamos começar avaliando a energia potencial gravitacional, cuja formulinha é parecida com a da força gravitacional, sendo:
Em que é a constante gravitacional universal, e são as massas do par de corpos envolvidos ,e é a distância entre esse par de corpos.
A gente sempre vai avaliar a interação gravitacional em pares de corpos, mesmo em sistemas com mais de 2 corpos. Daí depois a gente soma tudo (ou calcula as forças resultantes, dependendo do caso) pra todos os corpos, beleza?
Passo 2
a.Calculando a pra cada par, nas unidades do sistema internacional, a gente tem:
Entre a partícula do vértice de cima e a do vértice esquerdo da base:
Entre a partícula do vértice de cima e a do vértice direito da base:
Entre as partículas dos vértices da base:
Bom, nenhum mistério que daria tudo igual, né?
Uma vez que cada partícula está no vértice de um triângulo equilátero e todas têm a mesma massa, isso era de se esperar.
Assim, a energia potencial gravitacional total do sistema é exatamente a soma desses valores, sendo:
Passo 3
Gente, pelo esqueminha do Passo 1, a gente verifica que a força resultante que agiria em cada partícula devido a presença das outras duas partículas, respectivamente, apontaria pro centro do triângulo equilátero, que por sua vez está sempre inscrito em uma circunferência.
Nisso, essa força resultante aponta pro centro dessa circunferência, sendo portanto uma força resultante do tipo centrípeta!
Se elas forem soltas, então, vão em algum momento colidir no centro do triângulo, ou no centro da circunferência desenhada!
Resposta
a.
b.No centro da circunferência/do triângulo equilátero