Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 70
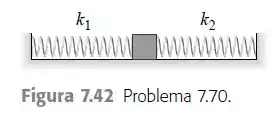
Um bloco de está conectado a duas molas ideais horizontais com constantes de força e (Figura 7.42). O sistema está inicialmente em equilíbrio
sobre uma superfície horizontal, sem atrito. O bloco é empurrado para a
direita e libertado do repouso. (a) Qual é a velocidade escalar máxima do bloco? Em que ponto do movimento essa velocidade máxima ocorre? (b) Qual é a compressão máxima da mola 1?
Passo 1
(a) Oi, galerinha! Tudo bom? A grande sacada aqui é perceber que quando o bloco 2 está comprimido, o 1 está estendido!
Como estão em repouso, só há energia pontencial elástica inicialmente.
Para achar a velocidade máxima do bloco, temos que ela vai ocorrer quando toda energia elástica se transformar em cinética!
Passo 2
Então, por conservação de energia, temos:
Como vimos, tanto quanto serão 15cm, a diferença estaria no sinal do , pois uma está comprimida e a outra está estendida. Porém, como elevamos o ao quadrado, o sinal não vai nos interessar.
Substituindo os valores na equação da energia, passando tudo para o SI:
Simplificando a equação:
Passo 3
(b) Para achar a compressão máximo temos que nos ligar que se a velocidade máxima ocorre quando toda a energia elástica se transforma em energia cinética, a compressão máxima ocorre quando toda a energia cinética se transforma em elástica!
Então, seria fazer o caminho contrário da letra anterior, chegando numa compressão máxima de . Ficaria assim ó:
Como , já que a diferença é apenas que quando uma tá comprimida a outra tá estendida no mesmo valor, ficamos com:
No fim do dia, teríamos:
Resposta
- a compressão máxima da mola 1 é de .