Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 74

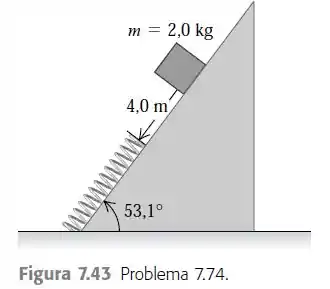
Um pacote de 2,0 kg inicialmente em repouso é abandonado sobre um plano inclinado de 53,1°, a uma distância de 4,0 m de uma mola com constante de 120 N/m presa à base do um plano (Figura 7.43). Os coeficientes de atrito entre o pacote e o plano inclinado são dados por μ = 0,40 e μ c = 0,20 . A massa da mola é desprezível. a) Qual é a velocidade do pacote imediatamente antes de colidir com a mola? b) Qual é a compressão máxima da mola? c) O pacote é rebatido para cima do plano inclinado. Qual é a distância entre o ponto inicial e o ponto onde ele pára momentaneamente?

Passo 1

Olá, amigo. Yuri aqui estarei te ajudando a resolver essa atividade.

Vamos analisar o enunciado e identificar os pontos importantes:

Dados Iniciais:

- Massa do pacote (m): 2,0 kg

- Ângulo do plano inclinado (θ): 53,1°

- Distância do pacote até a mola (d): 4,0 m

- Constante elástica da mola (k): 120 N / m

- Coeficientes de atrito: μ   =   0,40 e μ c   =   0,20

- Massa da mola: desprezível

Inicialmente temos uma caixa, em repouso, largada a 4 cm da mola, ela possui energia potencial gravitacional e é ela que irá atuar na caixa inicialmente.

Vamos aplicar a equação:

K 1 + U 1 + W o u t r a = K 2 + U 2

para o pacote.

W o u t r a = W f k

o trabalho realizado pelo atrito cinético.

Sabemos que:

f k = μ k N = μ k m g cos ⁡ θ

Com θ = 53,1 ° .

Seja L = 4,00   m , a distância que a embalagem se move antes atingindo a mola e seja a compressão máxima da mola. Seja o ponto 1 a posição inicial do pacote, o ponto 2 é exatamente como ele entra em contato com a mola, o ponto 3 é a compressão máxima da mola e o ponto 4 ser a posição final do pacote depois que ele se recuperar.

Passo 2

  1. Como K 1 = 0 ,   U 2 = 0 .

    2. A velocidade do pacote imediatamente antes de colidir com a mola é resultante da energia armazenada pelo potencial gravitacional e a energia perdida para o trabalho da força de atrito.

    W o u t r a = - f k L = - μ k L cos ⁡ θ

    U 1 = m g   L sen ⁡ θ

    E

    K 2 = 1 2 m v 2

    onde   v é a velocidade antes que o bloco atinja a mola.

    A equação K 1 + U 1 + W o u t r a = K 2 + U 2

    aplicado aos pontos 1 e 2, com y 2 = 0 , temos que:

    U 1 + W o u t r a = K 2

    Resolvendo para v :

    v = 2 g L ( sen ⁡ θ - μ k cos ⁡ θ )

    = 2 ⋅ 9,8 m / s 2 ⋅ 4 m ⋅ ( sen ⁡ 53,1 ° - 0,20 ⋅ cos ⁡ 53,1 ° )

    = 7,3 m / s

    Passo 3

  2. Aplicando a equação K 1 + U 1 + W o u t r a = K 2 + U 2 aos pontos 1 e 3.

    3. Tomando y 3 = 0 .

    K 1 = K 3 = 0

    Sabemos que:

    U 1 = m g L + d sin ⁡ θ

    E

    U 2 = 1 2 k d 2

    Assim,

    W o u t r a = - f k L + d

    A equação K 1 + U 1 + W o u t r a = K 2 + U 2   nos dá que:

    m g L + d sen ⁡ θ - μ k m g cos ⁡ θ L + d = 1 2 k d 2

    Isso pode ser escrito como:

    d 2 k 2 m g ( sen ⁡ θ - μ k cos ⁡ θ ) - d - L = 0

    O fator multiplicador d 2 é 4.504 m - 1 e usando Baskhara, temos que:

    d = 1,06 m

    Passo 4

  3. A coisa mais fácil a fazer aqui é reconhecer que a presença da mola determina d , mas no final do movimento a mola não tem energia potencial, e a distância abaixo do ponto de partida é determinada apenas pela forma como muita energia foi perdida por atrito.

Se o bloco terminar uma distância y abaixo do ponto inicial, então o bloco moveu uma distância L + d abaixo da inclinação e L + d - y acima da inclinação.

A magnitude da força de atrito é igual em ambas as direções, μ k   m g   c o s θ , e, portanto, o trabalho realizado por atrito é - μ k   ( 2 L + 2 d - y ) m g   c o s θ .

Isto deve ser igual à mudança na energia potencial gravitacional, que é - m g y s i n θ .

Igualar esses valores e resolver y   fornece:

y = L + d 2 μ k cos ⁡ θ sen ⁡ θ + μ k cos ⁡ θ = L + d 2 μ k tan ⁡ θ + μ k

Usando o valor de d encontrado na parte b) e os valores fornecidos para μ k e θ , temos que:

y = 1,32 m

Resposta

  1. v = 7,3 m / s
  2. d = 1,06 m
  3. y = 1,32 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12,0 k g está a 2,0m acima do solo (Figura 7.36 ). Use o princípio da conservação da energia para achar a velocidade dessa lata quando ela atinge o solo. Despreze o atrito e a inércia da polia.
Gravidade em três dimensões. Uma massa m 1 é mantida no ponto de origem e outra massa m 2 está livre para percorrer uma distância r a partir de um ponto P com coordenadas x, y e z. Aenergia potencial
Quanta energia total é armazenada no lago do Problema 7.79? Como naquele problema, considere a energia potencial gravitacional como igual a zero na base da represa. Expresse suaresposta em joules e em
Uma força conservativa F atuando ao longo do eixo Ox e uma força dada pela lei de Hooke F = - k x atuam sobre um íon.a) Mostre que uma possível função energia potencial para a combinação dessas forças
Um bloco de gelo de 0,150 kg é colocado contra uma mola horizontal comprimida no alto de uma mesa de altura 1,20 m acima do solo. A mola está inicialmente comprimida 0,045 m e a constante da mola é ig