Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 7.Problemas - Ex. 57

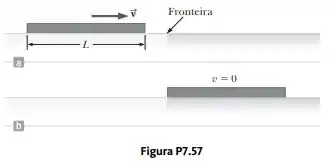
Uma tábua uniforme de comprimento L está deslizando ao longo de um plano horizontal suave e sem atrito, como mostrado na Figura P7.57a. A tábua então desliza através do limite com uma superfície horizontal áspera. O coeficiente de atrito cinético entre a tábua e a segunda superfície é μ k . (a) Encontre a aceleração da tábua no momento em que sua parte dianteira tenha viajado uma distância x além da divisa. (b) A tábua para no instante em que sua traseira atinge a divisa, como mostrado na Figura P7.57b. Encontre a velocidade inicial v da tábua.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

Seja m a massa de toda a tábua. A parte da superfície áspera tem massa m x L . A força normal que o suporta é m x g L e a força de atrito é μ k m g x L = m a . Então:

a = μ k g x L   o p o s t o   a o   m o v i m e n t o

Passo 2

Letra b:

Em um movimento infinitesimal para a frente dx, a energia cinética convertida em energia interna é:

f k d x = μ k m g x L d x

A energia total convertida é:

1 2 m v 2 = ∫ 0 L   μ k m g x L d x = μ k m g L x 2 2 0 L = μ k m g L 2

v = μ k g L

Resposta

  1. a = μ k g x L   o p o s t o   a o   m o v i m e n t o
  2. v = μ k g L
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco de plástico de 75 g é arremessado de um ponto 1,1 m acima do solo, com uma velocidade escalar de 12 m/s. Quando o disco atinge uma altura de 2, 1 m, sua velocidade é 10,5 m/s. Qual é a reduçã
Um jogador de beisebol arremessa uma bola com uma velocidade inicial de 81,8m i / h . Imediatamente antes de outro jogador segurar a bola na mesma altura, sua velocidade é 110p é s / s é . De quanto é
Você empurra um bloco de 2,0k g contra uma mola horizontal, comprimindo-a 15c m . Em seguida, solta o bloco e a mola o faz deslizar sobre uma mesa. O bloco para depois de percorrer 75c m a partir do p
Na Fig. 8-55, um bloco é liberado a partir do repouso a uma altura d=40c m , desce uma rampa sem atrito e chega a um primeiro trecho plano, de comprimento d , onde o coeficiente de atrito cinético é 0
Quando um besouro salta-martim está deitado de costas, pode pular encurvando bruscamente o corpo, o que converte a energia armazenada em um músculo em energia mecânica, produzindo um estalo audível. O