Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 7.Problemas - Ex. 80
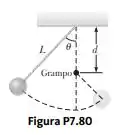
Um pêndulo, englobando um barbante leve de comprimento e uma pequena esfera, balança em um plano vertical. O barbante bate em um grampo localizado a uma distância embaixo do ponto de suspensão (Fig. P7.80). (a) Mostre que, se a esfera for solta de uma altura abaixo daquela do grampo, ela voltará para essa altura depois que o barbante bate no grampo. (b) Mostre que, se o pêndulo é solto do repouso na posição horizontal () e balança em um círculo completo centrado no grampo, o valor mínimo de d deve ser .
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
Letra a:
A energia é conservada no balanço do pêndulo, e o grampo estacionário não faz nenhum trabalho. Portanto, a velocidade da bola não muda quando o barbante atinge ou deixa o grampo, e a bola balança igualmente alto em ambos os lados.
Passo 2
Letra b:
A bola vai balançar em um círculo de raio Rsobre o grampo. Se a bola é para viajar no círculo, a aceleração centrípeta mínima no topo do círculo deve ser o da gravidade:
Quando a bola é lançada do repouso, e quando está no topo do círculo, , onde a altura é medida a partir da parte inferior do balanço. Por conservação de energia:
A partir disso e da condição em , encontramos .
Resposta
- A energia é conservada no balanço do pêndulo, e o grampo estacionário não faz nenhum trabalho. Portanto, a velocidade da bola não muda quando o barbante atinge ou deixa o grampo, e a bola balança igualmente alto em ambos os lados.
- .