Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 5
Um vetor velocidade abaixo do semi-eixo positivo tem um componente de . Qual é o valor de seu componente ?
Passo 1
Nosso primeiro passo vai ser desenhar a situação, beleza? Isso ajuda muitoo
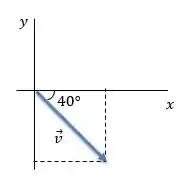
Na figura temos um vetor velocidade, que eu chamei de , ele está abaixo do semi-eixo positivo e o ângulo que ele forma com esse eixo é igual a .
O problema nos fornece também o valor da componente desse vetor, então bora decompor ele:
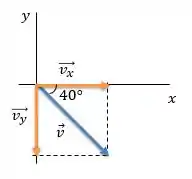
Lembra daquele macetinho? A componente que está COlada com o ângulo é igual ao módulo do vetor vezes o COsseno do ângulo. Já a componente que está SEparada do ângulo é igual ao módulo do vetor vezes o SEno do ângulo.
Então vamos ter que:
Nota que para a componente tem um sinal de negativo acompanhando. Esse sinal é pra indicar que essa componente está apontando no sentido contrário ao sentido do eixo . Beleza?
Passo 2
Como conhecemos podemos utilizar essa fórmula:
Para encontrar o valor do módulo, , do vetor:
Lembrando que:
Temos:
Passo 3
Agora que conhecemos o módulo do vetor, podemos usar essa fórmula:
Para encontrarmos o valor de .
Lembrando que:
Então, temos:
E é isso =)