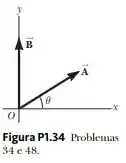
Use o método das componentes para adicionar os vetores e mostrados na Figura P1.34. Expresse o resultante na notação de vetor unitário.
Passo 1
Fala ai gente! Bora resolver mais uma questão?
Precisamos das componentes do vetor pois ele está inclinado em um sistema de coordenadas e o vetor B tem direção vertical.
Passo 2
Temos que:
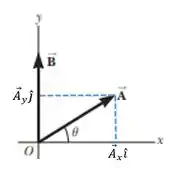
Sendo:
E:
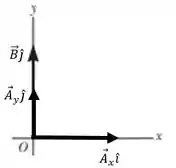
O somatório das forças nos eixos .
O vetor resultante é, portanto.