Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 49
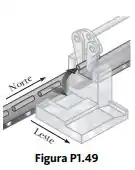
Em uma operação de montagem ilustrada na Figura P1.49, um robô move, primeiro, um objeto em linha reta para cima e, depois, também para o leste, em torno de um arco formando um quarto de um círculo de raio de , que se situa em um plano vertical leste-oeste. O robô então move o objeto para cima e para o norte, através de um quarto de círculo de raio , que se situa no plano vertical norte-sul. Encontre
a) o módulo do deslocamento total do objeto
b) o ângulo que o deslocamento total forma com a vertical.
Passo 1
Fala ai pessoal tranquilo? Bora fazer mais uma questão?
- Através da imagem vocês podem ver que o objeto é colocado para o lado e depois é jogado de forma a percorre um meio arco da circunferência. Sendo assim, ele percorre seu próprio comprimento e depois percorre um raio de Sendo assim o deslocamento será
- O ângulo formado pode ser calculado através da seguinte equação
Passo 2
Utilizando uma calculadora o arco tangente de é °
Resposta
- 35,5°
Exercícios de Livros Relacionados
Um sólido cristalino consiste em átomos empilhados em uma estrutura de treliça repetitiva. Considere um cristal conforme mostrado na Figura P1.53a. Os átomos residem nos cantos de cubos de lado L=0,20
Uma topógrafa mede a largura de um rio em linha reta pelo método a seguir (Fig. P1.55). Começando diretamente em frente a uma árvore na margem oposta, ela andad=100 m ao longo da margem para estabelec
Conforme pega seus passageiros, uma motorista de ônibus atravessa quatro deslocamentos sucessivos representados pela expressão – 6,30b i ^–4,00bc o s40 ° i ^–4,00bs e n40 ° j ^+3,00bc o s50 ° i ^–( 3,
Um paralelepípedo retangular tem dimensões a ,b e c , como mostrado na Figura P1.71.a) Obtenha uma expressão para o vetor da face diagonal R 1 → .b) Qual é o módulo desse vetor?c) Observe que R 1 → ,
Um vetor tem um componente x de– 25,0 unidades e um componente y de 40,0 unidades. Encontre o módulo e a direção e o sentido desse vetor.