Campo Magnético Gerado por uma Bobina
Teoria
Campo Magnético Gerado por uma Espira
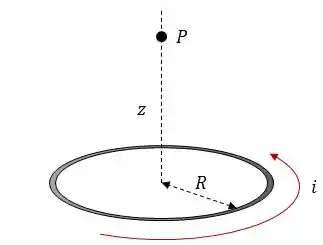
A situação agora é a seguinte...Temos uma espira circular de raio e que transporta uma corrente elétrica , conforme a figura abaixo:
No tópico de fios infinitos nós escrevemos o campo magnético pela lei de Biot-Savart como
Vamos começar considerando o comprimento da figura abaixo.
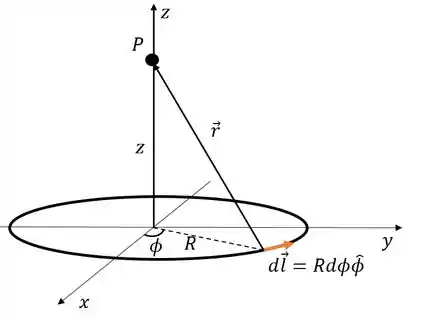
Em coordenadas cilindricas esse é
Ou seja, vamos integrar em , de a , percorrendo todo o fio.
Pelo triângulo retângulo da figura, a distância entre cada ponto do fio até o ponto é dada por
Assim ficamos com
Como vamos integrar em então podemos tirar tudo que tem e da integral
Repara que eu deixei o produto vetorial pro final! Isso por que essa é a parte mais importante!
Aqui a gente tá trabalhando em coordenadas cilindricas. Se fosse pra fazer esse produto vetorial bonitinho a gente precisaria escrever os vetores e em função de , e . Só que isso daria um trabalhão! Pra isso vamos usar a regra da mão direita!
Desenhando os vetores e , o produto vetorial deles seria algo assim
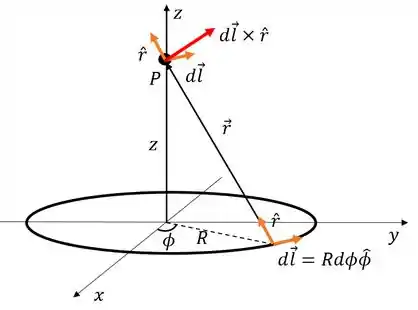
Lembrando que tem que ser perpendicular tanto a quanto a . Esse vetor tá numa direção meio esquisita. O máximo que a gente consegue fazer é separar ele em uma projeção na direção e outra projeção na direção .
Lembra de uma situação parecida com o campo elétrico de um fio circular? Se a gente calcula o campo elétrico produzido por um fio com densidade linear homogênea de carga o campo elétrico no centro do fio tem que apontar na direção , lembra? Isso por que quando a gente soma todas as componentes de todos os pedacinhos do fio o campo no plano se anula e só sobra o campo na direção . Algo parecido acontece aqui!
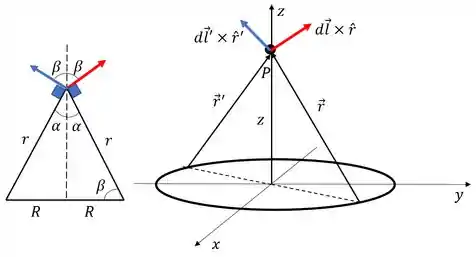
Se pegarmos dois pontos do fio diametralmente opostos e somarmos os campos dos dois teremos um campo resultante na direção ! E como a gente expressa isso? Basta corrigir a nossa equação projetando o campo na direção e afirmando por meio do que a gente explicou aqui que o campo pela simetria aponta na direção ! Lembre-se de explicar isso tim tim por tim tim sempre, hein!
Pra projetar na direção , basta multiplicar pelo cosseno de desenhado na figura. Como o campo magnético tem que ser perpendicular a é só ir completando os ângulos pra chegar que aparece nos triângulos retângulos da parte esquerda da figura. Assim
Beleza! Agora o nosso campo fica
Ainda bem que apareceu uma integral fácil!!!!!!
Juntando tudo
O sentido do campo magnético é o mesmo sentido do momento dipolo magnético, e pode também ser determinado pela regra da mão direita (MAS isso é só um macete pra lembrar e não a justificativa formal!!!!), onde a sua mão deve acompanhar o sentido da corrente, e o campo magnético estará na mesma direção e no mesmo sentido do seu dedão, beleza?
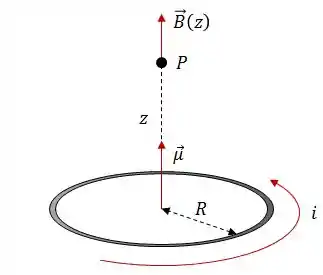
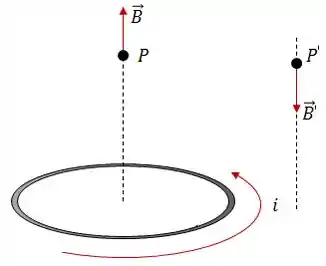
OBS.: Essa regra da mão direita é válida apenas para pontos que pertencem a eixos que passam pelo interior da espira. Para pontos que pertencem a eixos que passam fora da espira, a direção determinada pelo dedão se inverte. Vamos observar a figura abaixo:
Para pontos muito distantes , o campo magnético gerado pode ser aproximado para:
Já no centro da espira , tem-se:
Campo Magnético Gerado por uma Bobina
Podemos aproveitar a relação a que chegamos acima e escrever o campo magnético em função de .
Já sabemos que uma bobina nada mais é do que espiras “umas sobre as outras”, percorridas por uma corrente elétrica . Assim, o campo magnético gerado em um ponto em que será dado por:
O momento dipolo magnético é dado por:
A área da espira é dada por:
Logo:
Substituindo na expressão do campo magnético, teremos:
Bora lá treinar?
Campo Magnético Gerado por uma Bobina
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 229-56- Modificado.
A figura abaixo mostra um fio que conduz uma corrente e forma uma bobina circular com apenas uma espira. Na figura um fio de mesmo comprimento forma uma bobina circular com duas espiras de raio igual à metade do raio da espira da figura .
Se e são os módulos dos campos magnéticos nos centros das duas bobinas, qual é o valor da razão ?
Qual é o valor da razão entre os momentos dipolares das duas bobinas?
Passo 1
Vamos lá, galera! Nesse exercício, temos uma bobina circular com uma espira que conduz uma corrente e que tem um raio que chamaremos de .
Temos também uma segunda bobina, só que essa é formada por duas espiras de raio .
Primeiramente, queremos saber a razão entre os campos no centro das bobinas, .
Passo 2
Sabemos que o módulo do campo magnético a uma distância do centro de uma bobina de N espiras é dado por:
Logo, quando , temos:
Assim:
Passo 3
O momento dipolar magnético de uma bobina é dado por:
Assim,
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 229-58- Modificado.
A figura abaixo mostra um dispositivo conhecido como bobina de Helmholtz, formado por duas bobinas circulares coaxiais de raio , com espiras, separadas por uma distância . As duas bobinas conduzem correntes iguais no mesmo sentido. Determine o módulo do campo magnético no ponto , situado sobre o eixo das bobinas, a meio caminho entre elas.
Dados:
Passo 1
Então, galera! Temos duas bobinas de 200 espiras, com correntes iguais e mesmo raio . Queremos saber o campo magnético num ponto P que equidista, ou seja, está a mesma distância das duas bobinas.
Passo 2
Sabemos que o campo magnético gerado por uma bobina de uma espira num ponto a uma distância é dado por:
Como as correntes têm o mesmo sentido, as duas bobinas produzem campos iguais com o mesmo sentido (pela regra da mão direita, encontramos que é o sentido .
Assim, passando para as unidades SI:
Resposta
Exercício Resolvido #3
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 28.32, pp. 274
Uma bobina circular de espiras enroladas de modo compacto possui raio de .
- Qual deve ser a corrente que passa pela bobina, supondo que o campo magnético no centro da bobina é igual a ?
- A que distância do centro da bobina, sobre o eixo da bobina, o campo magnético é igual à metade de seu valor no centro?
Passo 1
Fala aíííííííí....Vamo lá? Antes de começar a questão de fato, bora discutir um pouco da situação física que a gente tem no exercício, blz?
A gente tem uma bobina condutora com espiras enroladas e empilhadas umas sobre as outras de forma bastante compacta. “Bastante compacta” significa que a distância do centro de cada uma das espiras até o ponto tem o mesmo valor !! Blz?
Então, o módulo campo magnético produzido pela bobina no ponto sobre o eixo de simetria da bobina pode ser calculado como vezes o campo produzido em por uma única espira, ou seja,
Passo 2
a) O exercício fornece , R e no centro da bobina e pede para encontrarmos a corrente que produz esse campo. Portanto, organizando a equação acima, temos
Passo 3
b) Neste item, precisamos encontrar a distância tal que
Simplificando essa expressão, obtemos os seguinte:
Substituindo os valores fornecidos pelo enunciado, chegamos que as distâncias são:
Nessas posições, o campo magnético é igual à metade do campo magnético produzido no centro da bobina em .
Resposta
- ;
- .
Exercício Resolvido #4
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exemplo 28.6, pp. 255
Uma bobina conduzindo uma corrente de é constituída por espiras circulares enroladas de modo compacto, cada uma com raio igual a .
- Determine o módulo do campo magnético ao longo do eixo da bobina, situado a uma distância de do seu centro.
- Em que ponto ao longo do eixo da bobina o campo magnético se reduz a do valor do campo no centro da bobina?
- Determine o valor do momento de dipolo magnético que pode ser associado à essa bobina.
Passo 1
A gente tem uma bobina condutora com espiras enroladas e empilhadas umas sobre as outras de forma bastante compacta. Isso significa que a distância do centro de cada uma das espiras até o ponto tem o mesmo valor !! Blz? Então, o módulo campo magnético produzido pela bobina no ponto sobre o eixo de simetria da bobina pode ser calculado como vezes o campo produzido em por uma única espira, ou seja,
sendo que o módulo do campo magnético produzido por uma única bobina é
Guarda essa expressão no seu coração aí, porque ela aparece, hein?!! ;-)
Sigamos...
Passo 2
a) Se você substitui os valores fornecidos lá no enunciado, a gente o seguinte:
Tranquilo, né? Só substituir os valores lá do enunciado. \0/
Passo 3
b) Neste item, precisamos encontrar a distância tal que
Simplificando essa expressão, obtemos:
Portanto,
Essas são as posições nas quais o campo magnético é igual a do campo magnético produzido pela corrente no centro da bobina, em .
Passo 4
c) O momento magnético que pode ser associado à essa bobina pode ser escrito como
sendo qua nessa expressão é a área de cada uma das esprias da bobina, tranquilo? Seguindo e colocando os valores do enunciado, temos
Esse é o valor do dipole magnético associado à bobina de espiras.
Resposta
- ;
- ;
Exercício Resolvido #5
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 28.34, pp. 274
Uma bobina circular com espiras enroladas de modo compacto possui raio igual a e conduz uma corrente de . Quantas espiras ela deve ter para que o módulo do campo magnético seja de em um ponto sobre o eixo da bobina afastado de de seu centro?
Passo 1
De tanto estudar os exercícios de fixação aqui que preparamos, você já tá careca de saber que, se a gente tem uma bobina condutora com espiras enroladas e empilhadas umas sobre as outras de forma bastante compacta, então a distância do centro de cada uma das espiras até o ponto tem o mesmo valor !! Blz?
Por isso (“lá vem ele repetir essa história tooooda de nooovo...” ): o módulo campo magnético produzido pela bobina no ponto sobre o eixo de simetria da bobina pode ser calculado como vezes o campo produzido em por uma única espira, ou seja,
Passo 2
Como estamos interessados no número de espiras , podemos isolar essa quantidade na expressão acima para o módulo e obter
Resposta
Exercício Resolvido #6
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 28.67, pp. 277.
A figura abaixo mostra a seção reta de duas bobinas circulares com raio , cada uma delas com espiras que conduzem uma corrente no mesmo sentido. A distância entre as bobinas é igual ao raio das bobinas. As bobinas dessa configuração denominam-se bobinas de Helmholtz e produzem um campo magnético bastante uniforme na região entre elas. O ponto está à mesma distância do centro de cada uma das duas bobinas.
- Deduza uma expressão para o módulo do campo magnétido em um ponto situado a uma distância à direita do ponto , que está no centro de simetria das bobinas.
- Usando a expressão obtida no item a), obtenha o módulo do campo magnético exatamente sobre o ponto .
- Calcule o valor do módulo do campo magnético no ponto , considerando espiras, e .
Passo 1
A gente viu várias vezes aqui durante os exercícios de fixação, que o módulo campo magnético produzido por uma bobina compacta no ponto sobre o eixo de simetria, abaixo ou acima do plano da bobina, pode ser calculado como vezes o campo produzido em por uma única espira, ou seja,
Note que, independente de o ponto estar à esquerda ou direita do plano da bobina, o campo magnético no ponto aponta na direção e sentido de , pois tomamos o sentido da corrente como está indicado na figura. Tranquilo? Dá uma checada nisso, porque isso é muito importante para a gente resolver este exercício aqui!! Guarda no coração isso...\0/
Passo 2
a) Bom, pra gente obter uma expressão para o campo no ponto a uma distância à direita do ponto da figura, precisamos notar que, a espira da esquerda produz um campo magnético no ponto que é dado por
e a espira da direita produz um campo magnético em dado por
Portanto, como os dois campos acima apontam na mesma direção e sentido dado por , o campo resultante no ponto à direita de é tem a seguinte expressão:
Essa é a expressão geral para o módulo do campo magnético em qualquer ponto sobre o eixo que passa pelo centro das duas bobinas!
CUIDAAAADOOOOOO: tá escrito aí que: “CAMPO MAGNÉTICO EM QUALQUER PONTO SOBRE O EIXO QUE PASSA PELO CENTRO DAS DUAS ESPIRAS SEPARADAS POR ”
Fica de olho nisso...
Passo 3
b) Para gente saber como é o campo no ponto , basta fazer na expressão acima para , o que nos dá o seguinte:
Se simplificamos essa expressão, obtemos que
Passo 4
c) Com os valores dados no enunciado, encontramos que o campo no ponto tem o seguinte valor
Resposta
Exercício Resolvido #7
Sears & Zemanske, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12ª ed., São Paulo: Addison Wesley, 2009, Problema 28.33, pp. 274
Uma bobina circular com 600 espiras enroladas de modo compacto possui diâmetro igual a 4,0 cm e conduz uma corrente de 0,500 A. Qual é o módulo do campo magnético (a) no centro de bobina? (b) em um ponto sobre o eixo da bobina afastado 8,0 cm de seu centro.
Passo 1
Para resolver essa questão, basta lembramos da fórmula do campo magnético gerado por uma bobina:
Como o problema só pede o módulo desse campo, vamos ficar com a seguinte fórmula:
Sendo R o raio da espira, e z a distância do centro da espira até um determinado ponto.
Passo 2
Na letra (a), como estamos no centro da espira, e a nossa fórmula ficara assim:
Agora substituímos, lembrando que . E que . Temos:
Passo 3
Na letra (b), vamos fazer a mesma coisa mas temos que .
Portanto, temos:
Substituindo:
Lembrando que o campo magnético tem seu valor máximo no centro. Portanto nossas respostas estão coerentes! =)
Resposta
(a)
(b)
Exercício Resolvido #8
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 9ª edição. Rio de Janeiro: LTC, 2012, pp 244
Qual é o módulo do momento dipolar magnético de um solenoide de 200 espiras, 25 cm de comprimento, 10 cm de diâmetro e corrente 0,29 A?
Passo 1
Essa é uma questão muito simples, basta lembrarmos da formula do momento dipolo magnético em uma bobina:
Onde é o número de espiras da bobina, é a corrente e é a área da espira.
Passo 2
Como temos espiras circulares:
Temos que:
E ficamos com a seguinte expressão:
Substituindo os valores: