Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Circuito RL

Ver Todos os Exercícios

Teoria

Fala aí! Bora trocar uma ideia sobre circuitos RL e como podemos relacionar esses caras com indutores? Vem comigo!

Ah, se quiser dar uma revisada mais completa em indutores e indutância, não deixa de conferir o primeiro link aqui embaixo, junto com alguns outros que podem ser muito úteis pra você. 👇😉

Aqui vou passar bem por cima, pra podermos ir logo ao que interessa, beleza?

⭐ Veja também ⭐

E se preferir, estude esse conteúdo por meio desse nosso vídeo maravilhoso, ou segue comigo na sequência!

Indutores

Lá em indutores e indutância, a gente vê que um indutor é um dispositivo capaz de gerar variações de fluxo magnético em um circuito. A indutância é a capacidade desses dispositivos induzirem uma força eletromotriz.

Pra lembrar como se calcula a indutância, devemos usar essa fórmula aqui:

👉 é a indutância (medido em Henry (H)).

👉 é a corrente elétrica.

👉 é o enlace do fluxo.

Esse tá relacionado com uma outra expressão:

👉 é o fluxo magnético.

Quando temos uma espira (tal como os indutores que veremos logo mais), vale 1.

Por último, mas não menos importante, temos a força eletromotriz auto-induzida:

O aí, nesse caso, é o que chamamos de autoindutância.

Essa última equação vai ser a mais importante aqui pra gente, e já te mostro por quê.

Indutores em Série

É importante sabermos que os indutores podem ser associados de maneira muito similar à associação de resistores.

Se liga no seguinte circuito RL:

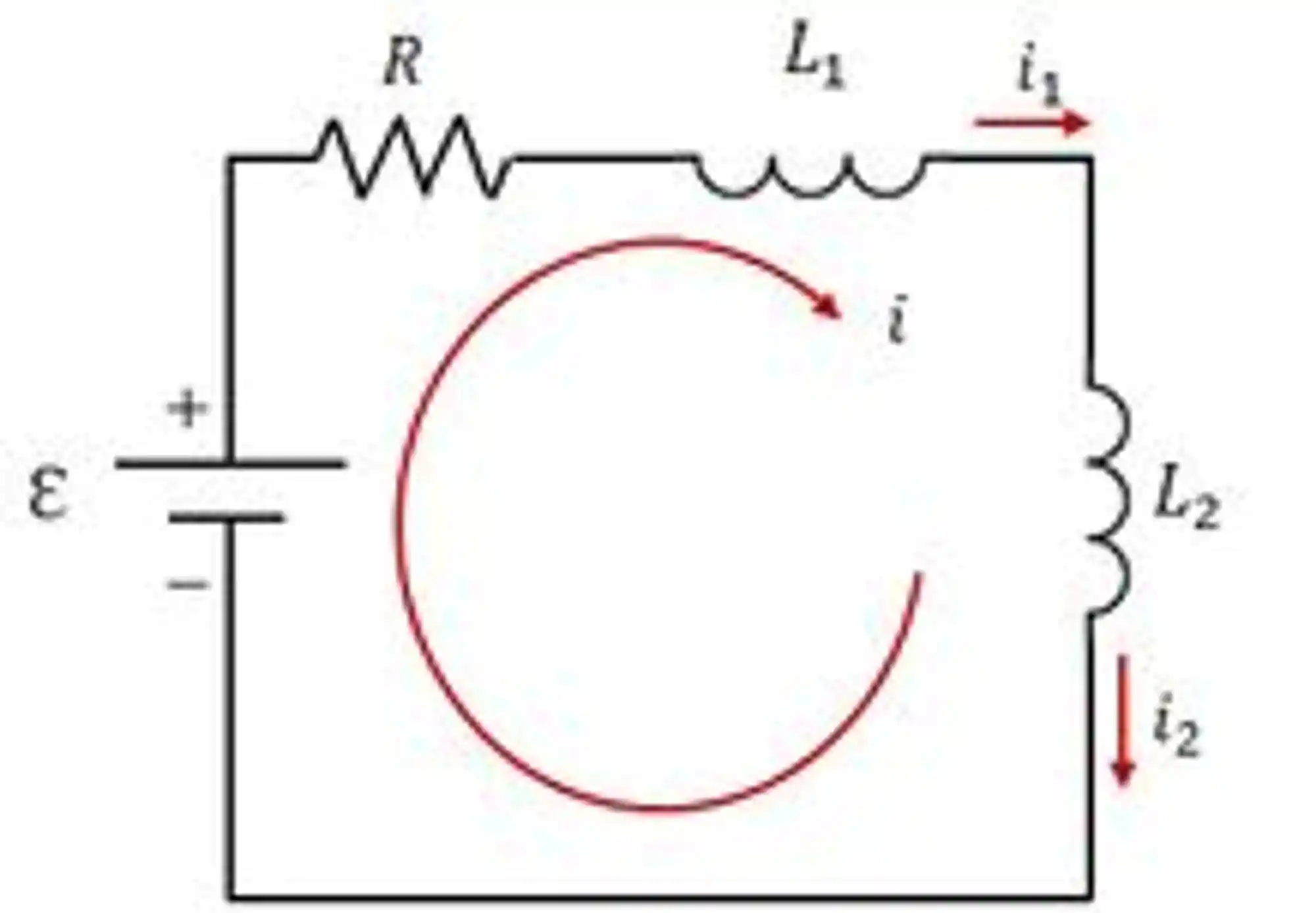
Circuito RL com indutores em série.
Circuito RL com indutores em série.

Os indutores são aqueles carinhas em espirais ali ( e ). A indutância equivalente, para indutores em série, pode ser dada por:

Indutores em Paralelo

Agora, nesse circuito aqui:

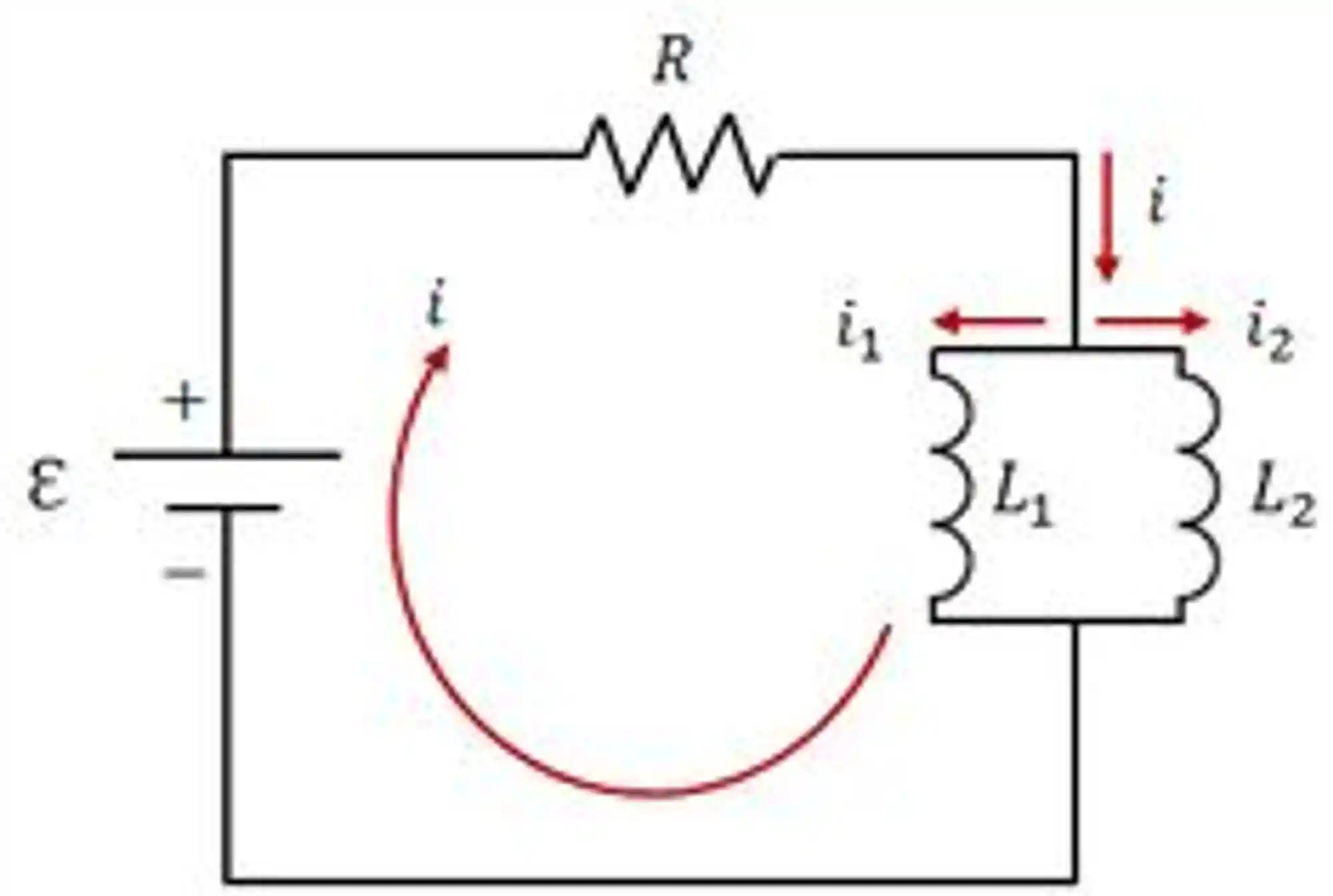
Circuito RL com indutores em paralelo.
Circuito RL com indutores em paralelo.

Para indutores associados em paralelo, como na figura acima:

Como funciona um circuito RL?

Agora sim, você tem todas as informações necessárias para entender como funciona um cara desse tipo!

O circuito RL é todo circuito composto por resistores e indutores. Um bem simplesinho tem essa cara aqui:

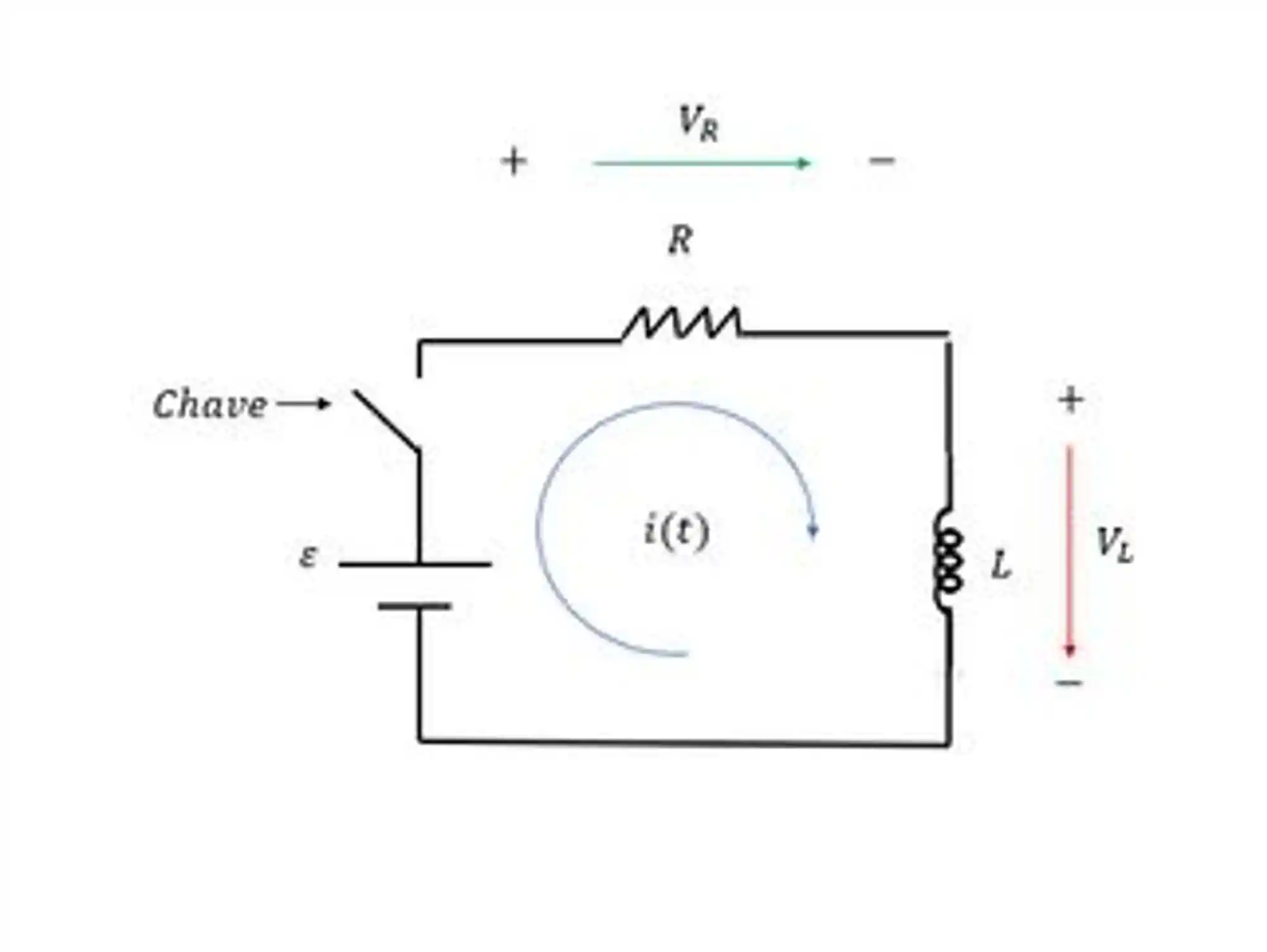
Exemplo de um circuito RL.
Exemplo de um circuito RL.

Aquela espiral (solenoide) é como representamos o indutor. Vamos descobrir se tem alguma novidade disso aí para os circuitos RC (Resistência + Condutor) e qual o impacto daquela chave representada ali no diagrama.

Carregamento do Indutor

Enquanto a chave está aberta, o indutor está totalmente descarregado, já que não há circulação de corrente. É como se, para a chave, o circuito estivesse aberto no local do indutor.

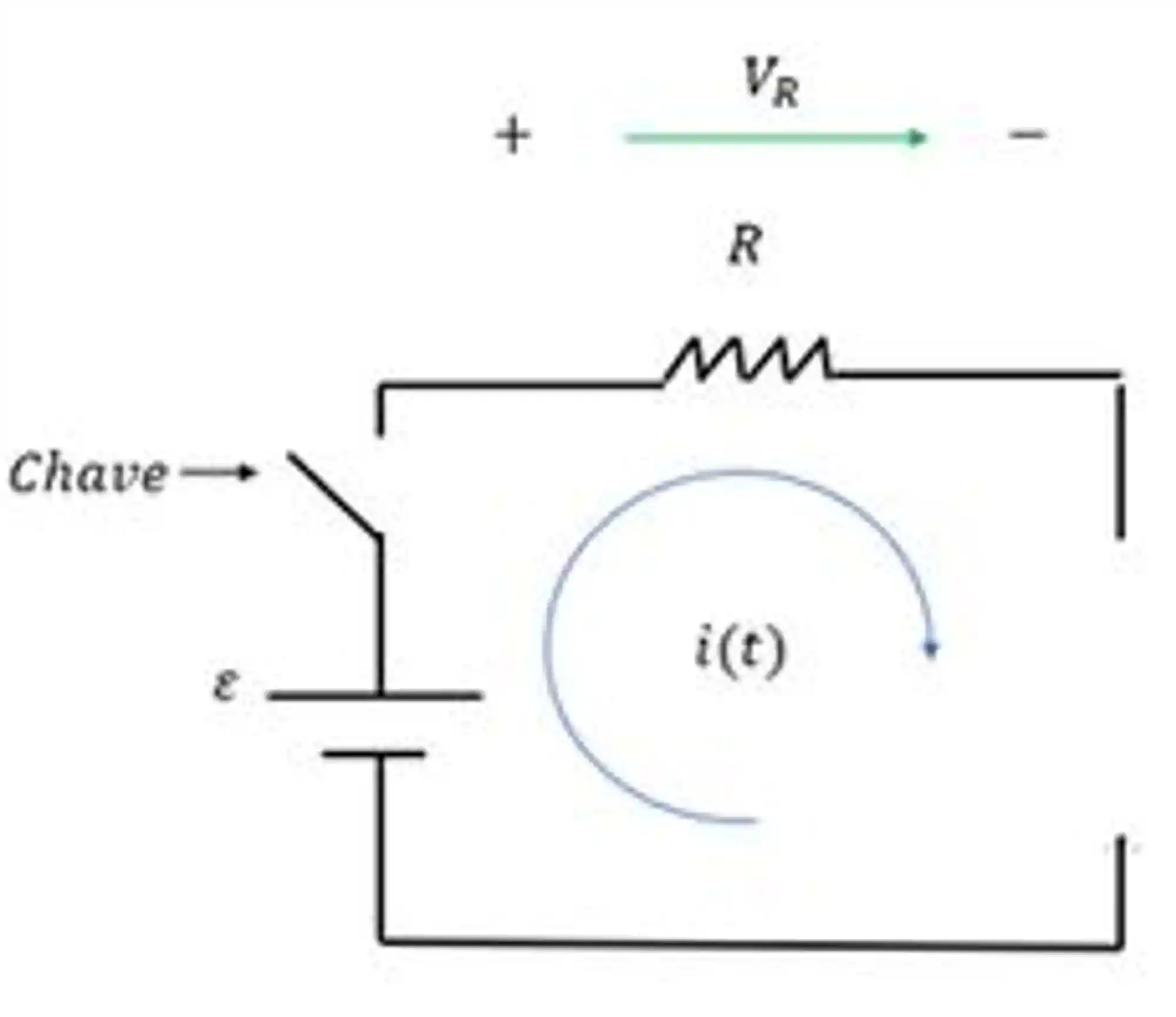
O circuito com a chave aberta.
O circuito com a chave aberta.

Quando fechamos a chave no tempo , o indutor demora um pouquinho pra “perceber” isso e continua trabalhando como aberto.

Quando, finalmente, o circuito passa a se comportar como fechado, temos que analisar a variação do potencial quando percorremos o circuito no sentido da corrente:

  • Resistor R: Ao passar pelo resistor, o potencial varia .
  • Indutor L: Ao passar pelo indutor, o potencial varia .
  • Fonte: Ao passar pela fonte, percorrendo do polo negativo para o positivo, o potencial varia .

Com isso, pela lei das malhas:

Se isolarmos a corrente:

Repare que:

  • Para , a corrente é zero.
  • Para , a corrente é .

Assim, podemos esboçar o gráfico i x t.

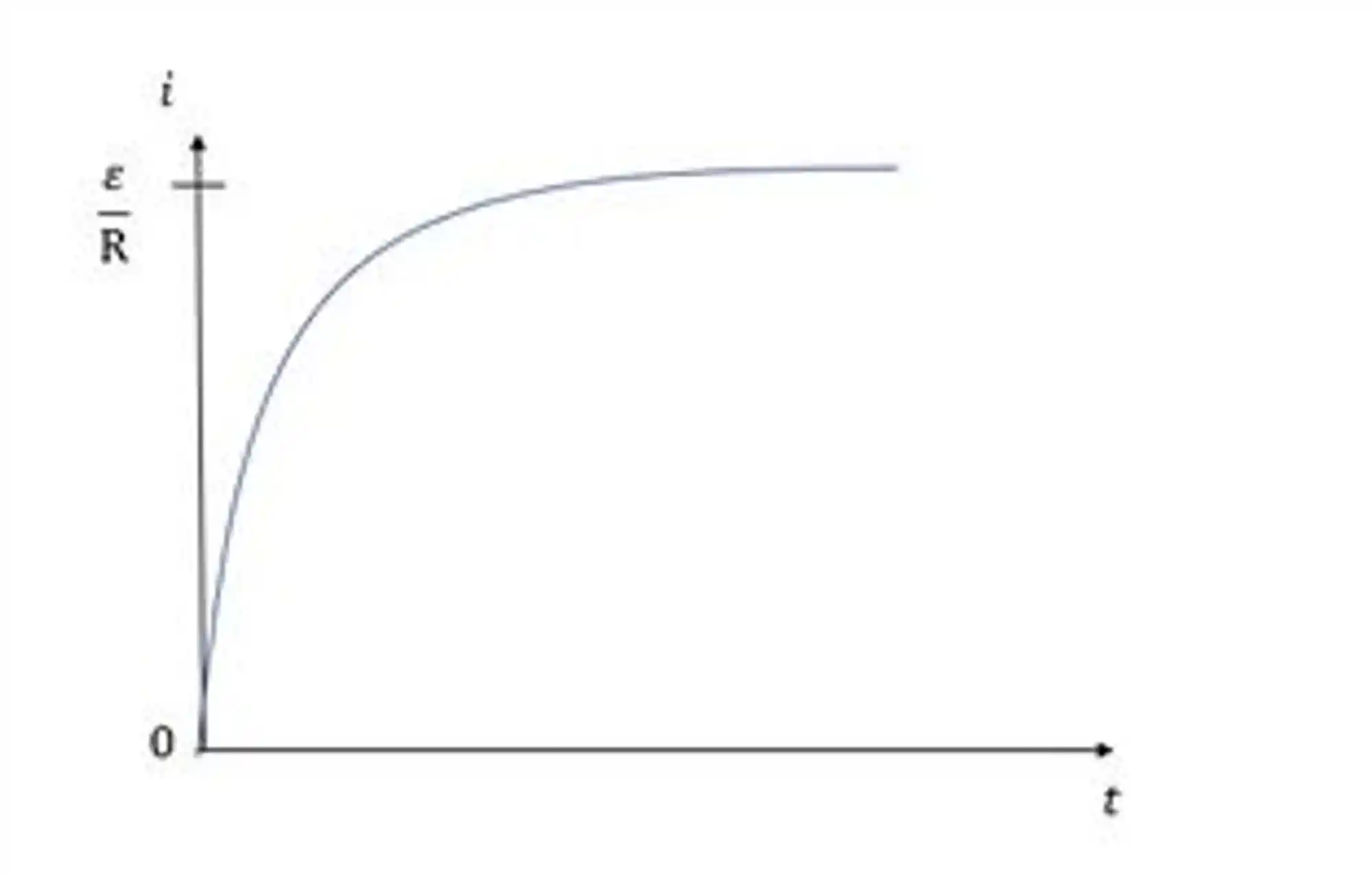
Gráfico da corrente em função do tempo.
Gráfico da corrente em função do tempo.

E a voltagem pode ser encontrada da seguinte forma:

E o gráfico da voltagem fica assim:

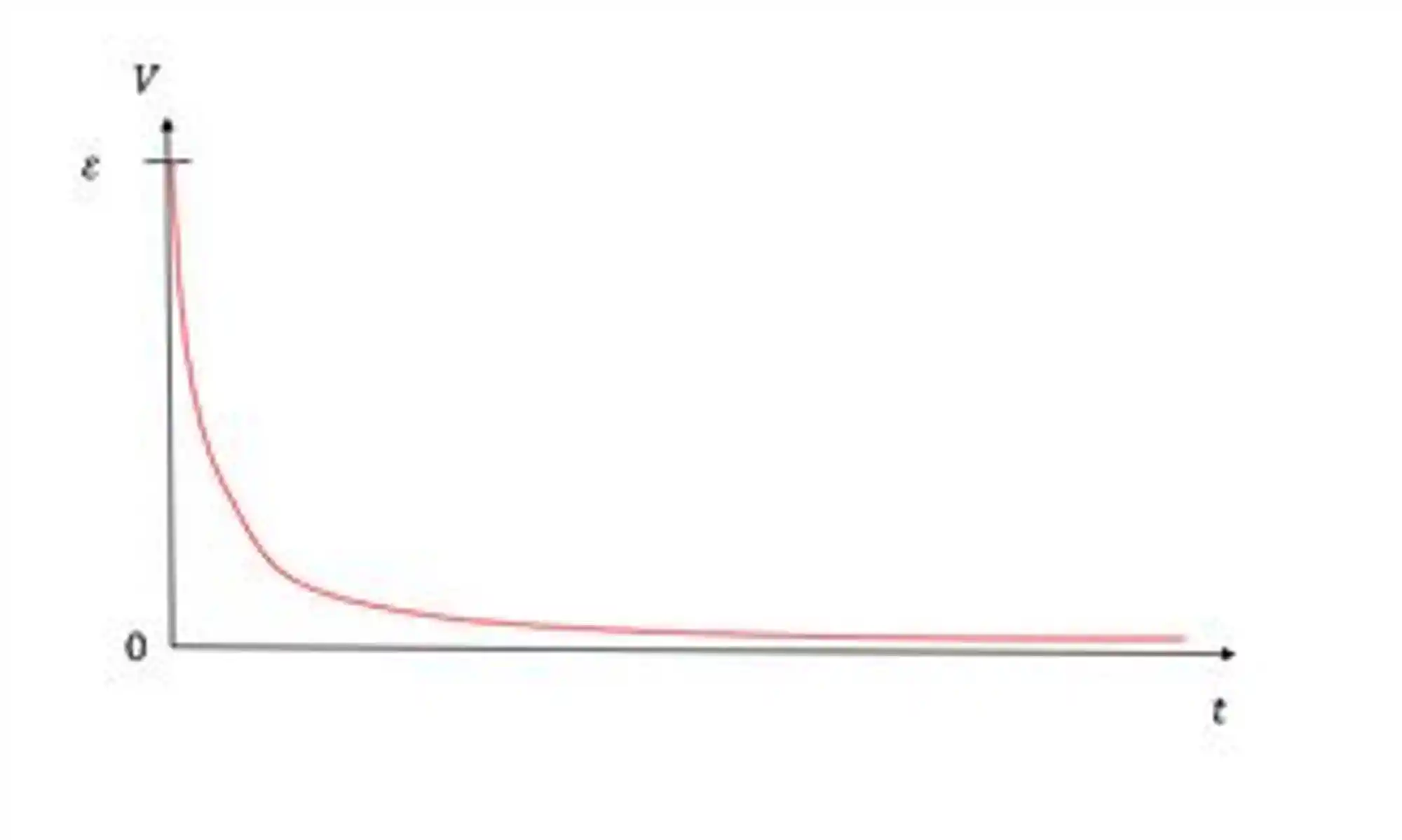
Gráfico do potencial em função do tempo.
Gráfico do potencial em função do tempo.

Descarregamento do Indutor

Ao retirarmos a bateria do circuito, a corrente não cessa imediatamente. O indutor irá se opor à variação de corrente e o circuito fica assim:

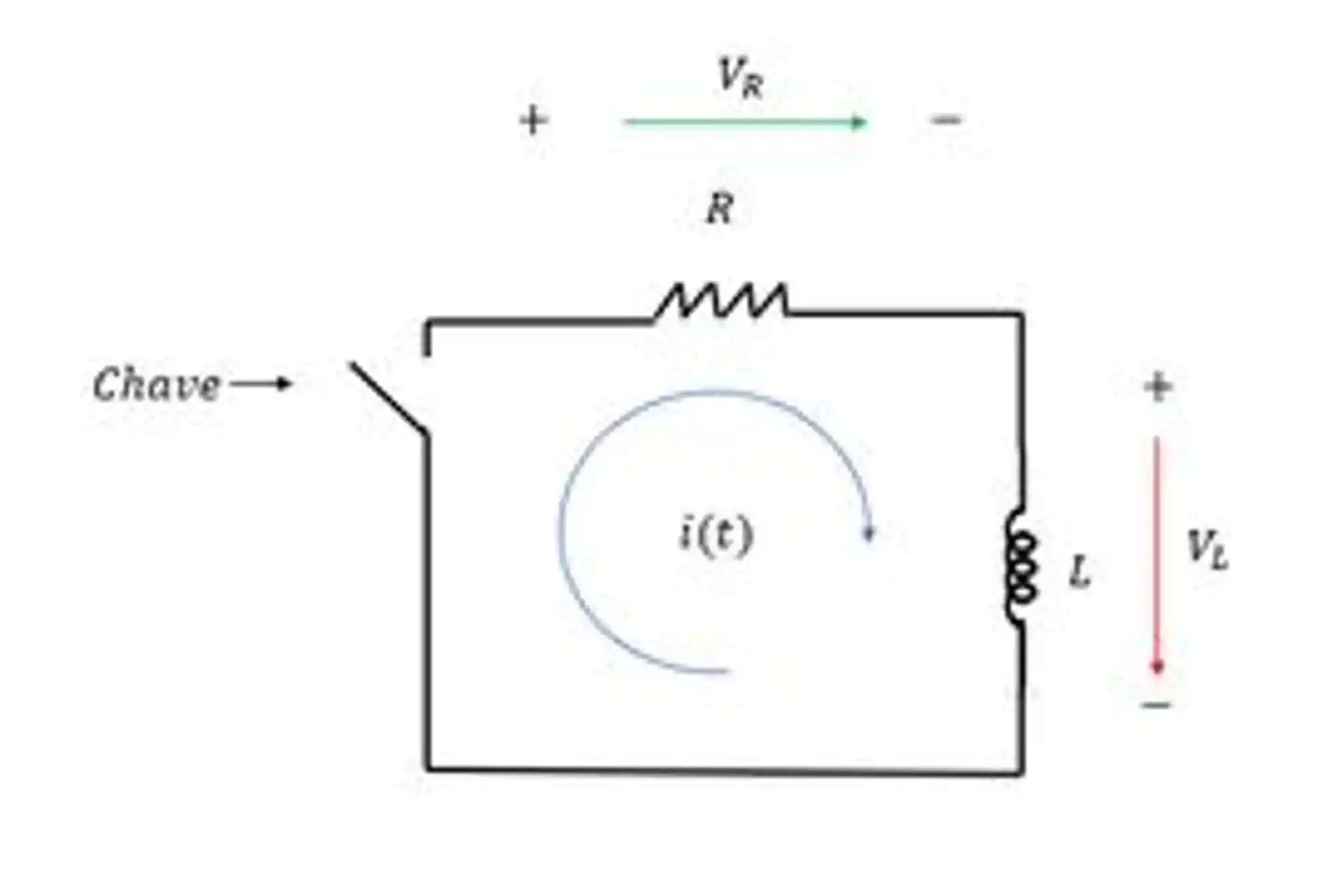
Circuito após removida a fonte.
Circuito após removida a fonte.

Neste momento, o indutor está carregado. Mas quando a chave for fechada, o indutor começa a descarregar.

A lei das malhas, agora sem bateria, é essa aqui:

A gente ainda pode aplicar a lei de Ohm no resistor:

Com isso:

Bom, por hoje é só! Não deixa de conferir nossos exercícios resolvidos pra ficar bem craque nesse assunto!

Carregamento do Indutor

Descarregamento do Indutor

Exercícios Resolvidos

Exercício Resolvido #1

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 298-49 - Modificado.

O circuito de indutores da figura abaixo, com L 1 = 30,0   m H , L 2 = 50,0   m H , L 3 = 20,0   m H e L 4 = 15,0   m H , é ligado a uma fonte de corrente alternada. Qual a indutância equivalente?

Passo 1

Bom, temos que calcular a indutância equivalente do circuito da figura.

O que precisamos lembrar é que quando temos mais de um indutor em um circuito, eles podem estar associados em série ou em paralelo, beleza? E é muito importante a gente identificar essa associação para podermos calcular a indutância equivalente.

Então bora analisar: Podemos observar pela figura que L 2 e L 3 estão em paralelo, e o indutor equivalente dessa associação estará em série com L 1 e L 4 .

Passo 2

Primeiro, vamos calcular o indutor equivalente, L e q 1 , da associação em paralelo de L 2 e L 3 . Sabemos que a indutância equivalente de uma associação em paralelo é dada pela fórmula:

1 L e q = 1 L 1 + 1 L 2

Assim, teremos:

1 L e q 1 = 1 L 2 + 1 L 3 = 1 50 + 1 20 = 7 100

Logo,

L e q 1 = 100 7

O circuito equivalente será assim:

Passo 3

Agora, podemos perceber que L 1 , L e q 1 e L 4 estão em série. Para uma associação em série a indutância equivalente é dada pela fórmula:

L e q = L 1 + L 2

Assim, teremos:

L e q = L 1 + L e q 1 + L 4 = 30 + 100 7 + 15 = 59,3   m H

E o circuito equivalente será assim:

E desse modo conseguimos reduzir o circuito com quatro indutores a um circuito com um único indutor equivalente, L e q = 59,3   m H

Resposta

59,3   m H

Exercício Resolvido #2

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 298-51

Uma bateria é ligada a um circuito R L em série no instante t = 0 . Para que múltiplo de τ L a corrente atinge um valor 0,1   % menor que o valor final?

Passo 1

Em um circuito R L , a corrente varia com o tempo de acordo com a equação abaixo:

i = E R 1 - e - t τ L

Quando t → ∞ , a corrente será E / R . Assim, a corrente atinge um valor 0,1   % menor que o valor final quando:

i = 99,9 % E R

i = 0,999 E R

Assim, basta substituir isso na equação da corrente e calcular o valor de t .

Passo 2

0,999 E R = E R 1 - e - t τ L

Beleza, agora vamos organizando esse cara até encontrarmos o que queremos, show?!

0,999 = 1 - e - t τ L

e - t τ L = 0,001

- t τ L = ln ⁡ 0,001

- t τ L = - 6,9

t = 6,9 τ L

Resposta

t = 6,9 τ L

Exercício Resolvido #3

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 298-52

A corrente em um circuito R L aumenta para um terço do valor final em 5,0 s . Determine a constante de tempo indutiva.

Passo 1

A corrente em um circuito R L varia com o tempo de acordo com a equação abaixo:

i = E R 1 - e - t τ L

Quando t → ∞ , a corrente será E / R . Assim, a corrente atinge um terço do valor final quando:

i = 1 3 E R → i = E 3 R

Assim, basta substituir isso na equação da corrente e calcular o valor de τ L .

Passo 2

E 3 R = E R 1 - e - t τ L

A boa agora é dar uma arrumada até descobrirmos τ L .

1 3 = 1 - e - t τ L

e - t τ L = 2 3

- t τ L = ln ⁡ 2 3

- t τ L = - 0,405

τ L = t 0,405

Onde t = 5,0 s . Portanto:

τ L = 5 0,405

τ L = 12,33 s

Resposta

τ L = 12,33 s

Exercício Resolvido #4

UFF – Física III – Lista 5 – Questão nº12

Os diagramas mostram três circuitos com baterias idênticas, indutores idênticos e resistores idênticos. Classifique, de acordo com a corrente através da bateria, logo após o interruptor estar fechado, a partir do menor valor para o maior. Explique.

Passo 1

Para um circuito RL, temos que a corrente varia da seguinte maneira:

i = ε R 1 - e - R . t L

Para determinar o valor da corrente, assim que fechamos o interruptor, basta substituir t → 0 , desse modo, acharemos que a corrente é nula. Ou seja, assim que fechamos o interruptor, a corrente através do indutor será nula.

Beleza, agora vamos analisar cada caso por vez.

Passo 2

  • Circuito 1

    • Assim que o interruptor é fechado, a corrente através do indutor é nula. Como os resistores e o indutor estão em série, a corrente no circuito inteiro será nula.

    i 1 = 0

  • Circuito 2

    • Nesse caso, assim que o interruptor é fechado, a corrente passará inteira pelo resistor que está em paralelo com o indutor. Portanto, aplicando a Lei das Malhas:

    E - R i 2 = 0

    i 2 = E R

  • Circuito 3

A corrente agora vai passar somente pelos dois resistores, não passando pelo indutor. Logo, através da Lei das Malhas, teremos:

E - R i 3 - R i 3 = 0

E - 2 R i 3 = 0

i 3 = E 2 R

Finalmente, organizando do menor para o maior, teremos:

i 1 < i 3 < i 2

Resposta

i 1 < i 3 < i 2

Exercício Resolvido #5

Circuito RL

Na figura, a chave S ficou fechada por um tempo muito longo.

a ) Quais são as correntes através de R 1 e R 2 ?

b ) Qual é a energia armazenada no indutor?

A chave é então aberta em t = 0 .

c ) Escreva a expressão da corrente através do indutor em função do tempo;

d ) Calcule a ddp inicial t = 0 através do indutor;

Passo 1

a ) Quais são as correntes através de R 1 e R 2 ?

Depois que a chave fica fechada por muito tempo t → ∞ , a corrente no indutor tende a ficar constante o indutor passa a se comportar como um “pedaço de fio” comum. Então não devemos leva-lo em consideração nessa situação. Assim o nosso circuito vai ser as duas resistências em paralelo!

Logo:

i 1 = ε R 1 = 24 2 = 12   A

i 2 = ε R 2 = 24 6 = 4   A

Passo 2

b ) Qual é a energia armazenada no indutor?

A energia armazenada em um indutor é dada por:

U = L i 1 2 2

Substituindo os valores:

U = 0,4 2   12 2 = 28,8   J

Passo 3

c ) Escreva a expressão da corrente através do indutor em função do tempo;

Aplicando Lei das malhas na malha total de fora (excluindo o fio que contém a bateria), temos:

- i 1 . R 1 - L . d i 1 d t - i 2 R 2 = 0

Nesse caso, temos i 1 = i 2 . Logo:

i 1 . R 1 + L . d i 1 d t + i 1 R 2 = 0

A solução dessa equação é:

i 1 t = i 0 e - ( R 1 + R 2 ) t L

Onde L R 1 + R 2 pode ser substituído por τ L , que a denominada constante de tempo indutiva. Essa equação nos dá corrente no circuito!

Como após desligar a chave, a única fonte de d.d.p. é o indutor (por que ele tem uma energia armazenada) a corrente no instante t = 0 vai ser a corrente no indutor que vimos no passo anterior

i 0 = 12 A

Assim substituindo todos os nossos valores

i 1 t = 12 e - 20 t

Passo 4

d ) Calcule a ddp inicial t = 0 através do indutor;

Temos que a ddp no indutor é dada por:

V L = L d i 1 d t = L d d t i 0 e - ( R 1 + R 2 ) t L = - L R 1 + R 2 L i 0 e - ( R 1 + R 2 ) t L

V L = - R 1 + R 2 i 0 e - ( R 1 + R 2 ) t L  

Quando t = 0 :

L . d i 1 d t = - R 1 + R 2 i 0 = - 2 + 6 12

V L = - 96   V

Resposta

a )

i 1 = 12   A

i 2 = 4   A

b )

U = 28,8   J

c )

i 1 t = i 0 e - ( R 1 + R 2 ) t L

d )

- 96   V

Exercício Resolvido #6

UNICAMP – Física III – Prova 3 – Noturno – Questão nº3.

No circuito da figura abaixo, a chave S ficou na posição A por um tempo muito longo.

a ) Nesta condição, qual é a corrente no circuito?

Agora, S é subitamente movida de A para B em t = 0 .

b ) Calcule a d d p inicial através do indutor e através de cada resistor.

c ) Calcule a energia magnética inicial armazenada no indutor.

d ) Calcule a energia total dissipada nos resistores.

Passo 1

a ) Qual é a corrente no circuito?

Em um circuito R L , quando o indutor está conectado à fonte, a corrente no circuito obedece à função:

i = ε R . 1 - e - R t L

Depois que a chave fica na posição A por muito tempo t → ∞ , a corrente no indutor tende a ficar constante o indutor passa a se comportar como um “pedaço de fio” comum. Então não devemos leva-lo em consideração nessa situação.

Logo:

i = ε R = 12 12

i = 1   A

Passo 2

b ) Calcule a d d p inicial através do indutor e através de cada resistor.

Quando a chave é movida para a posição B , o circuito passa a ser formado somente pelo indutor e pelos resistores.

Nessa situação, a corrente no circuito é dada por:

i = ε R e q . e - R e q t L

A partir daqui já podemos começar a brincar.

A d d p nos resistores é dada por:

V R = R i = R ε R e q . e - R e q t L

E a d d p no indutor é dada por:

V L = - L d i d t = ε . e - R e q t L

Em t = 0 , teremos:

V R = R ε R e q = 12 × 12 12 + 12

V R = 6   V

V L = ε = 12   V

Passo 3

c ) Calcule a energia magnética inicial armazenada no indutor.

A energia magnética é dada por:

U L = L i 2 2

A corrente inicial do circuito é dada por:

i = ε R e q = 12 12 + 12

i = 0,5   A

Logo:

U L = 2 × 0,5 2 2

U L = 0,25   J

Passo 4

d ) Calcule a energia total dissipada nos resistores.

Toda a energia armazenada no indutor será dissipada nos resistores, logo, a energia total dissipada nos resistores será:

U R = U L

U R = 0,25   J

Resposta

a )

i = 1   A

b )

V R = 6   V

V L = 12   V

c )

U L = 0,25   J

d )

U R = 0,25   J

Exercício Resolvido #7

Site do Prof. Gennady Gusev (USP), Capítulo 05, Circuitos RL e RC

As duas chaves do circuito que segue são fechadas em t = 0 . Determine i 1 ( t ) , i 2 ( t ) e i 3 ( t ) para t > 0 .

Passo 1

Antes de t = 0 , com o indutor em curto, temos que v L = 0 . Assim, a corrente i 3 ( t ) para t < 0 é dada por:

i 3 0 - = 0 .

Além disso, calculamos i 2 ( t ) para t < 0 pela lei das malhas:

- 0,2 + 10 i 2 + 10 i 2 + v L = 0 ,

20 i 2 = 0,2 → i 2 0 - = 0,01   A .

E também i 3 t para t < 0 :

- 0,3 + 20 i 1 + 40 i 1 + v L = 0 ,

60 i 1 = 0,3 → i 1 0 - = 0,005   A .

Por fim, calculamos i ( t ) para t < 0 como:

i 0 - = i 1 0 - + i 2 0 - = 0,015   A .

Passo 2

Após o fechamento das chaves, o indutor fica em paralelo com as resistências de 10   Ω e 40   Ω e as fontes deixam de alimentar o indutor, como na figura abaixo.

Assim, para t > 0 :

i 3 t = 0,2 10 = 0,02   A .

i 1 t = 0,3 20 = 0,015   A .

E o valor de i t será:

i t = i 0 - e - R L t ,

i t = 0,015 e - 8 0,8 t = 0,015 e - 10 t   A .

Passo 3

Para obter a corrente i 2 ( t ) para t > 0 , vamos olhar para a figura abaixo.

Temos que:

i 2 t + i x ( t ) = i t ,

onde chamamos de i x ( t ) a corrente que passa pelo resistor de 40   Ω .

Sabemos que a tensão nos dois resistores é a mesma. Logo:

10 i 2 t = 40 i x t ,

i x t = 1 4 i 2 t .

Substituindo:

i 2 t + 1 4 i 2 ( t ) = i t ,

5 4 i 2 t = i t → i 2 t = 4 5 i t ,

i 2 t = 0,012 e - 10 t   A .

Resposta

Para t > 0 :

i 1 t = 0,015   A ,

i 2 t = 0,012 e - 10 t   A ,

i 3 t = 0,02   A .

Exercício Resolvido #8

Site do Prof. Gennady Gusev (USP), Capítulo 05, Circuitos RL e RC

A chave da esquerda no circuito que segue é fechada em t = 0 .

(a) Determinar i L ( t ) e i 1 t para 0 < t < 0,15 .

(b) A chave do lado direito é fechada em t = 0,15 . Determine i L t e i 1 t para t > 0,15 .

Passo 1

(a) Determinar i L ( t ) e i 1 t para 0 < t < 0,15 .

Para t < 0 , temos que:

i 1 0 - = 0   A .

Além disso, o indutor está em curto e os resistores 2   Ω , 4   Ω e 6   Ω estão em série. Logo,

i L 0 - = 24 2 + 4 + 6 = 2   A .

Para 0 < t < 0,15 , com a chave da esquerda fechada, temos que:

i L t = i L 0 - e - R L t ,

onde o valor de R é dado pela soma das resistências 4   Ω e 6   Ω , já que estes resistores estão em série. Temos:

i L t = 2 e - 10 0,6 t = 2 e - 16,67 t   A .

Já para calcular i 1 ( t ) , utilizamos a lei das correntes:

i 1 t = 24 2 - i L t ,

i 1 t = 12 - 2 e - 16,67 t   A .

Passo 2

(b) Determine i L t e i 1 t para t > 0 , 15 .

Nesse caso, temos que:

i 1 t = 24 2 = 12   A ,

e

i L t = i L 0,15 e - 6 0,6 t ,

i L t = 2 e - 2,5 e - 10 t ,

i L t = 2 × 0,0821   e - 10 t ,

i L t = 0,1642 e - 10 t   A .

Resposta

(a) i L t = 2 e - 16,67 t   A e i 1 t = 12 - 2 e - 16,67 t   A .

(b) i L t = 0,1642 e - 10 t   A e i 1 t = 12   A .

Exercício Resolvido #9

Site do Prof. Renato B. Filho (Unicamp), Disciplina EA513, Capítulo 8, Circuitos Simplificados RC e RL

No circuito RL da figura abaixo, temos uma fonte de tensão controlada por corrente. Isso significa que sua diferença de potencial v ( t ) depende da corrente i t que circula pelo circuito. Calcule a constante de tempo indutiva e interprete o resultado.

Passo 1

Vamos analisar o circuito utilizando a Lei das Malhas. Temos que:

- i R - L d i t d t - k i t = 0 ,

d i t d t + R + k L i t = 0 .

Passo 2

A solução dessa equação nos dá que:

i t = i 0 e - R + k L t ,

logo, a constante de tempo será dada por:

τ L = L R + k .

E isso significa que a fonte dependente de corrente se comporta como um resistor de k   Ω .

Resposta

τ L = L R + k .

Exercícios de Livros Relacionados

Quanto tempo é necessário, depois que a fonta é removida, para que a diferença de potencial entre os terminais do resistor de um circuito RL com L = 2,00H e R = 3,00Ω diminua para 10,0 % do valor inic
Um gerador de frequência ajustável é ligado em série com um indutor L = 2,50m H e um capacitor C = 3,00μ F . Para que frequência o gerador uma corrente com a maior amplitude possível no circuito?
A força eletromotriz da fonte do circuito da Fig. 30-16 varia com o tempo de tal forma que a corrente é dada por i t = 3,0 + 5,0 t , onde i está em ampères e t em segundos. Suponha que R = 4,0Ω e L =
Na Fig. 30-70, depois que a chave S é fechada no instante t = 0 , a força eletromotriz da fonte é ajustada automaticamente para manter uma corrente constante i passando pela chave. (a) Determine a cor
Na figura 30-73a, a chave S permaneceu na posição A por um tempo suficiente para que a corrente no indutor de indutância L 1 = 5,00m H e o resistor de resistência R 1 = 25,0Ω se estabilizasse. Da mesm