Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.9 - Ex. 59
Na Fig. 30-70, depois que a chave é fechada no instante , a força eletromotriz da fonte é ajustada automaticamente para manter uma corrente constante passando pela chave. (a) Determine a corrente no indutor em função do tempo. (b) Em que instante a corrente no resistor é igual à corrente no indutor.
Passo 1
E aí, galerinha! 😬
O exercício apresentou um circuito em paralelo de modo que a corrente na chave permaneça constante e igual a . Vamos adotar a seguinte convenção de sentidos:
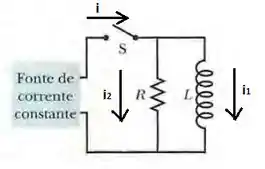
Assim, pela lei dos nós, temos que
Além disso, considerando a malha fechada composta pelo resistor e pelo indutor:
Temos que encontrar as correntes e como função do tempo. Para isso, isolamos na primeira equação:
Agora derivamos essa relação para obter
Usei que é constante, de modo que
Veja só! 😉
Passo 2
Substituindo a derivada de na segunda equação:
Resolvendo essa equação diferencial, obtemos a corrente no resistor como função do tempo:
Note que representa a corrente no resistor para . Assim, a corrente no indutor será
Agora, note uma coisa curiosa: em , toda a corrente deve estar no resistor, de modo que , assim
Vemos então que a corrente no fundo é a corrente constante que passa pela chave, de modo que
Tranquilo até aqui? 👀
Passo 3
A corrente no indutor será igual a corrente no resistor quando
Assim,
Tomando o log:
E aí! o que achou? Responde Aí! 😊
