Força Magnética sobre um Fio Condutor
Produzido por Bruno SoaresTeoria
Força em Corpos Carregados
Já sabemos como a força magnética age sobre cargas pontuais. Mas e quando estivermos falando de distribuições contínuas de carga?
Primeiramente vamos enxergar o que está acontecendo: temos uma distribuição contínua de cargas, todas elas com uma certa velocidade. Isto implica em estarmos falando de uma corrente , certo?
Nesse caso, a força resultante do campo externo nessa distribuição de cargas será dada por:
A sua dúvida agora é, naturalmente, o que significa esse vetor na equação. Esse vetor é tangente à trajetória das cargas puntiformes, ou seja, ele sempre aponta no sentido da corrente em determinado ponto.
Se tivermos um circuito, por exemplo:
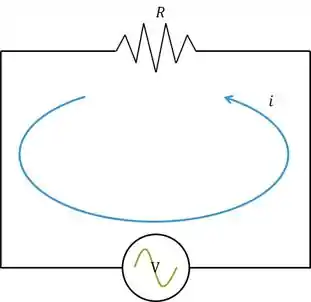
A trajetória você sabe: é só seguir o circuito no sentido da corrente, que é o anti-horário. Como ficaria o nesse caso?
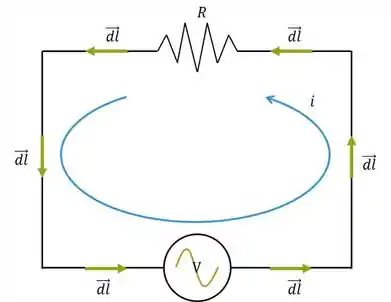
Beleza, tudo certinho até aqui? A única coisa chata é que esse novo vetor é (geralmente) uma variável. Mesmo drama daquele nas integrais de campo elétrico. Temos que tentar definir o sentido do produto vetorial, substituir, e tentar tratar na integral. Vamos rodar dois exemplos que resumem tudo o que você precisa saber sobre a orientação desse vetor doido.
Exemplo 1: Fio retilíneo
Começando com um caso simples, vamos imaginar só um pedaço do circuito de comprimento passando uma corrente . O campo magnético naquela região é uniforme e de módulo . Temos então:
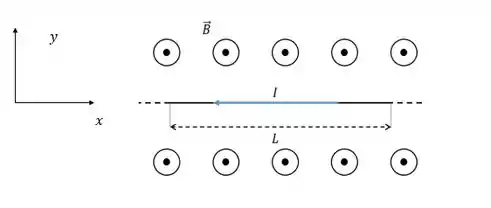
A questão é: qual a força que o campo faz nesse pedaço do circuito de comprimento ? Bom, vamos aplicar a fórmula já adaptada:
Podemos usar a regra da mão direita para determinar o sentido desse produto vetorial. No caso, vai ser para cima:
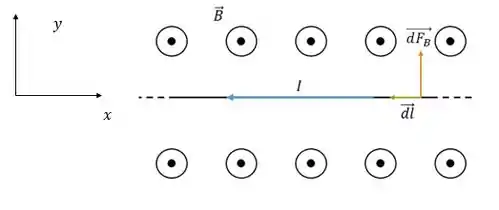
Como temos o eixo positivo para cima podemos dizer que o vetor está na direção . Agora que sabemos o sentido da força podemos ir integrando em todo o segmento do fio. Como o campo é uniforme e a corrente é constante ambos podem sair da integral:
A integral de pedaços infinitesimais do fio em um segmento de comprimento nada mais é o que :
Substituindo os valores temos:
E como :
No final das contas, sempre que estivermos trabalhando com um fio retilíneo, a força magnética sobre esse fio será dada por:
Onde é o vetor que tem o módulo igual ao tamanho do fio e a direção e sentido da corrente que passa por ele.
Exemplo 2: Fio semicircular
Agora vamos ver um caso com um variável. Se tivermos um fio em formato de semicírculo de raio com corrente constante e imerso numa região de campo magnético uniforme com módulo
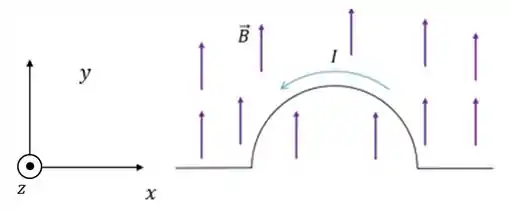
Qual a força magnética que o campo faz no segmento semicircular do fio? Bom, aplicamos a fórmula:
O que temos agora é um problema com o , mas isso não é muito estressante. Vamos desenhar vários deles e ver o que acontece:
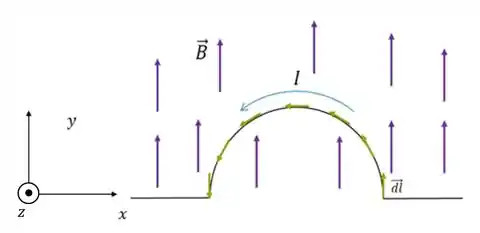
Note como a direção do produto vetorial é sempre a mesma:
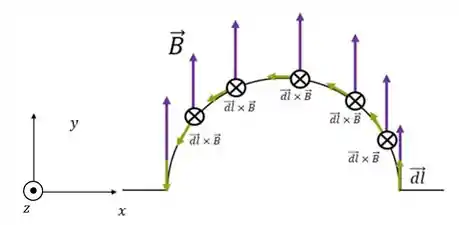
O que muda é o módulo. Se conseguirmos nos livrar desse vetor de dentro da integral o resto nós conseguimos tratar. Como foram mostrados os eixos, pela regra da mão direita vemos que o produto vai se dar para dentro do plano da página, na direção contrária ao eixo .
Agora precisamos tratar a integral:
Conforme dito no enunciado, o raio da semicircunferência é . Trocando para coordenadas polares:
Vemos também que o ângulo vai de até .
Ufa chegamos na equação da força magnética nesse caso:
Agora é só substituir os parâmetros e correr pro abraço:
Pronto.
Barras Deslizantes
Muitas vezes, nós iremos encontrar questões em que o fio não está fixo no espaço, e sim se movendo conforme uma força magnética atua sobre ele. Nosso trabalho, nesse tipo de problema, é determinar em que direção é o movimento do fio.
Chamaremos esse tipo de situação de barras deslizantes, mas na verdade não são as barras que se movem, é o fio. Se liga no exemplo!
Vamos analisar a seguinte situação:
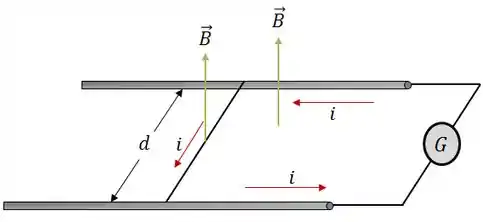
Nela, temos duas barras fixas horizontais, uma fonte de força eletromotriz e um fio retilíneo que une as duas barras e que pode se deslocar sem atrito sobre elas.
Todo o sistema está sobre a ação de um campo magnético que aponta para cima (direção perpendicular ao plano do circuito).
A partir do momento em que a corrente passa a circular no sistema, teremos uma força magnética atuando sobre o fio retilíneo. Essa força magnética fará o fio se mover.
Como faremos pra determinar a direção do movimento do fio?
Sabendo que a força resultante sobre a barra deslizante é a força magnética, podemos dizer, a partir da segunda lei de Newton, que:
Logo, a aceleração da barra será dada por:
Se quisermos calcular a velocidade, também não vamos ter que quebrar muito a cabeça. É só lembrar da fórmula da aceleração instantânea lá da cinemática:
Pra resolver essa integral, basta ficar de olho em quais termos são constantes pra tentar simplificar a sua vida.
Assim, se pararmos pra pensar, não foi tão difícil chegar nessas expressões, então talvez a boa seja entender o raciocínio que usamos aqui para que você possa fazer o mesmo. Pode ser melhor do que gravar mais fórmulas. Bora lá exercitar?
Exemplo 1: Fio retilíneo
Exemplo 2: Fio semicircular
Barras Deslizantes
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 228-40.
O fio dobrado da figura abaixo está submetido a um campo magnético uniforme. Cada trecho retilíneo tem de comprimento e faz um ângulo de com o eixo .
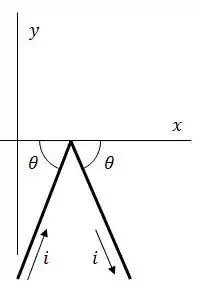
O fio é percorrido por uma corrente de . Qual é a força que o campo magnético exerce sobre o fio em termos de vetores unitários, se o campo magnético é:
;
;
Passo 1
;
Como os trechos retilíneos tem o mesmo comprimento, é uma boa tentarmos explorar a simetria do problema.
A força magnética sobre um fio retilíneo é dada por:
Aplicando a regra da mão direita, teremos o seguinte:

Analisando as forças, podemos perceber que as suas componentes na direção se anulam e as componentes na direção se somam.
A componente em sobre o primeiro fio será:
Logo:
Assim, a força resultante será:
Além disso, podemos ver que a força resultante estará apontando no sentido .
Passo 2
;
Novamente, partindo da regra da mão direita, podemos ver que, em ambos os fios, a força magnética estará apontando na direção , como mostra a figura abaixo.
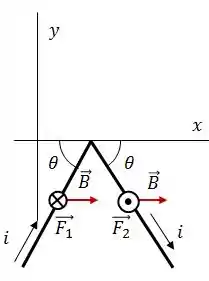
Como os dois fios são tem o mesmo tamanho, não é difícil concluir que .
Logo, as duas forças irão se anular e a força resultante total será nula:
Resposta
Exercício Resolvido #2
UFRJ – Física III – Prova 2 – 2014.1 – Múltipla Escolha nº3.
Calcule a força magnética resultante sobre o pedaço de fio, através do qual passa uma corrente elétrica estacionária de intensidade , composto por dois segmentos retilíneos, de comprimento , muito grande, e uma semicircunferência de círculo, de raio , na presença de um campo magnético constante (estacionário e uniforme) , .
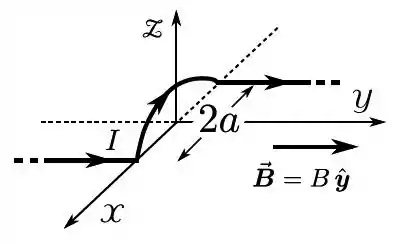
Passo 1
A força magnética é dada por:
No caso de uma distribuição contínua de cargas em movimento (corrente), utilizamos a expressão equivalente:
E integramos no circuito todo:
Basta determinarmos o sentido do produto vetorial para cada segmento. Podemos mostrar que para os retilíneos não há força por conta do produto nulo:
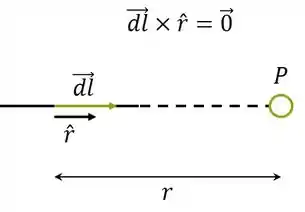
O que é conveniente, senão teríamos que fazer uma integral com limites de integração infinitos.
Passo 2
Fazendo agora o produto para o segmento semicircular:
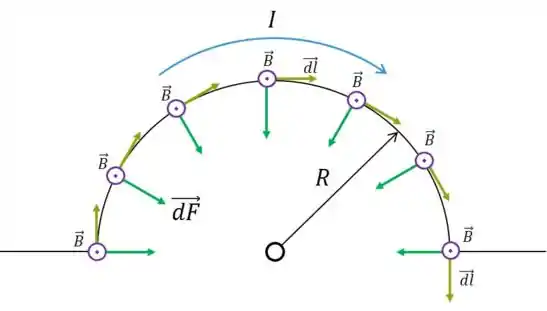
Podemos ver que sempre aponta para o centro, o que é uma pena. Nosso produto vetorial admite variabilidade, então não podemos tirar ele fora da integral... Por simetria sabemos que não vai haver componente no sentido de , como as respostas das múltiplas escolhas já sugerem.
Passo 3
Vamos decompor o vetor e achar a componente dela em :
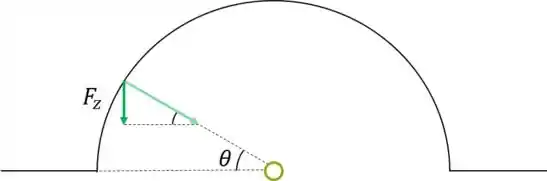
Calculando o módulo dele:
Trocamos para coordenadas polares:
Passo 4
Que resulta em:
Ajustamos o vetor para apontar pra baixo (pois já sabemos a orientação):
Resposta
Letra b
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 228-44.
Na figura abaixo, um fio metálico de massa pode deslizar com atrito insignificante sobre dois trilhos paralelos horizontais separados por uma distância .
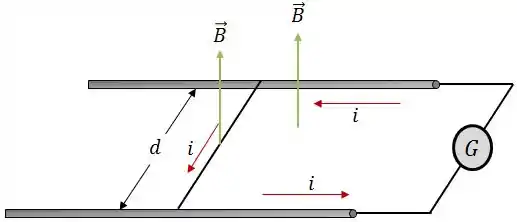
O conjunto está em uma região onde existe um campo magnético uniforme de módulo .
No instante um gerador é ligado aos trilhos e produz uma corrente constante no fio e nos trilhos (mesmo quando o fio está se movendo). No instante , determine:
a velocidade escalar do fio;
o sentido do movimento do fio (para a esquerda ou para a direita).
Passo 1
Determine a velocidade escalar do fio;
Sabendo que a força resultante sobre o fio deslizante é a força magnética, podemos dizer, a partir da segunda lei de Newton, que:
Logo, a aceleração da barra será dada por:
Como a corrente é constante, a aceleração também será constante. Portanto:
Como a velocidade inicial do fio é nula, teremos:
Onde:
Jogando isso tudo na expressão da velocidade, teremos:
Passo 2
Determine o sentido do movimento do fio (para a esquerda ou para a direita).
O sentido do movimento será dado pelo sentido da força magnética. Aplicando a regra da mão direita, teremos:
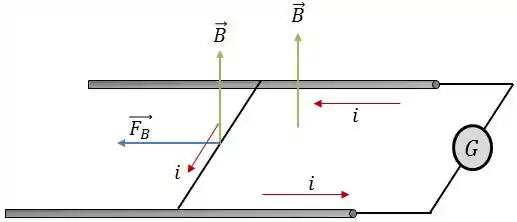
Logo, o fio se movimentará para a esquerda.
Resposta
O fio se movimentará para a esquerda.
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 228-45.
Uma barra de cobre de repousa em dois trilhos horizontais situados a de distância um do outro e é percorrida por uma corrente de . O coeficiente de atrito estático entre os trilhos é . Determine o módulo e o ângulo (em relação à vertical) do menor campo magnético que faz a barra se mover.
Passo 1
Beleza, esse não é dos mais fáceis, mas podemos dar conta numa boa...
Acontece que, como agora o campo magnético tem uma inclinação em relação à vertical, a força magnética sob a barra terá uma componente vertical e uma componente horizontal.
Antes de continuar, vamos definir como a componente horizontal do campo magnético e como a componente vertical do campo magnético, beleza? , por sua vez, é a força magnética gerada pelo campo magnético e , a força magnética gerada por .
Definindo o sentido da corrente indicado na figura, teremos a seguinte situação:
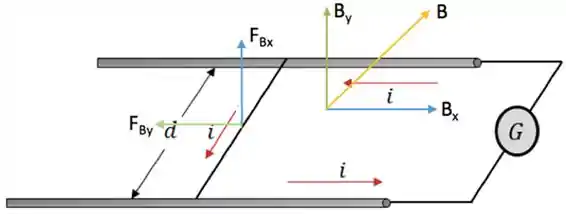
A menor força magnética na horizontal capaz de fazer o fio se mover deve ser igual à força de atrito estático. Logo:
Onde é o coeficiente de atrito estático e é a força normal.
Passo 2
A força normal é a reação entre a barra e os trilhos, logo:
Onde , portanto:
Passo 3
Fazendo o somatório de forças na horizontal, teremos:
Onde .
Como queremos descobrir o ângulo que o campo magnético faz com a vertical:
Jogando isso na equação de cima, teremos:
Reorganizando os termos, teremos o seguinte:
Beleza, mas o que faremos a partir daqui?
Passo 4
Para descobrir o ângulo em relação à vertical, vamos derivar a expressão de em relação e igualar o resultado a zero, beleza?
Dessa equação, , , , e são constantes, logo:
Para que essa razão seja nula, é necessário que o numerador seja nulo, portanto:
Onde :
Passo 5
Pra determinar o campo magnético, agora basta utilizar a relação de que encontramos no Passo 3.
Onde:
Jogando tudo em , teremos:
Resposta
Exercício Resolvido #5
UNICAMP – Física III – Prova 2 – 2012.2 – Diurno – Questão 4.
A figura abaixo mostra um fio que conduz uma corrente . Ele é formado por dois trechos retilíneos de comprimento , ambos tangentes à mesma circunferência de raio , e por um arco desta circunferência que subentende um ângulo central de , conforme a figura abaixo.
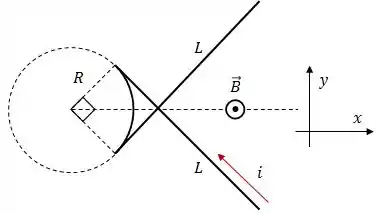
O fio está numa região onde existe um campo magnético uniforme, perpendicular ao plano da página e orientado para fora dela.
Calcule o vetor força magnética que age sobre cada segmento de fio retilíneo;
Calcule o vetor força magnética que age sobre a parte circular;
Calcule a força resultante que age sobre o fio;
Passo 1
Calcule o vetor força magnética que age sobre cada segmento de fio retilíneo;
A força magnética sobre uma espira é dada por:
No caso de um fio retilíneo e campo magnético uniforme, podemos dar uma simplificada na fórmula:
Lembrando que é o vetor que aponta sempre na direção e sentido da corrente.
Aqui, vamos dividir o problema em duas partes... vamos resolver para o fio 1 e para o fio 3, como mostra a figura.
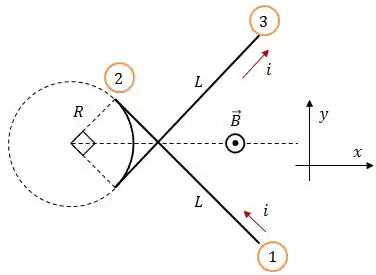
Passo 2
- Fio 1:
- Fio 3:
De acordo com o sentido que a corrente flui no fio 1, podemos escrever como:
Como o campo magnético é dado por , teremos:
De acordo com o sentido que a corrente flui no fio 3, podemos escrever como:
Assim, a força magnética sobre o fio 3 será:
Passo 3
Calcule o vetor força magnética que age sobre a parte circular;
A ideia aqui é começar calculando a força sobre um elemento infinitesimal do fio circular, como mostra a figura:
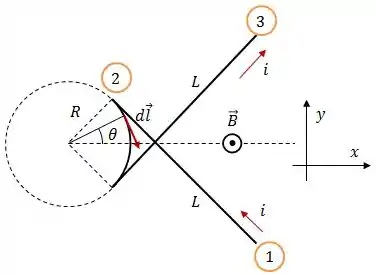
Logo:
Onde, de acordo com a figura acima:
Substituindo esses caras na expressão de , teremos:
Pra finalizar, temos apenas que integrar esse cara de até , seguindo o caminho da corrente, que vai de cima para baixo:
Onde:
Portanto:
Passo 4
Calcule a força resultante que age sobre o fio;
A força resultante no fio vai ser a soma vetorial das forças sobre os três fios, que nós já calculamos.
Agora é só organizar a bagunça:
Finalmente::
Resposta
Exercício Resolvido #6
UNICAMP – Física III – Prova 2 – 2012.2 – Noturno – Questão 4.
Um fio fino, transportando uma corrente , é dobrado na forma de um grampo composto por dois segmentos retilíneos de comprimento e um arco semicircular de raio .
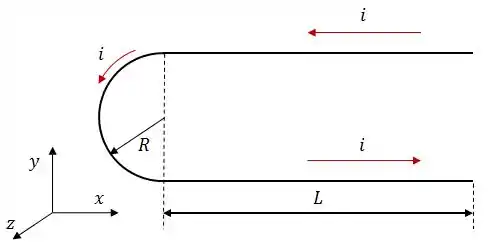
O fio está numa região onde existe um campo magnético uniforme, perpendicular ao plano do fio e orientado para fora da página, conforme figura ao lado.
- Calcule o vetor força magnética que age sobre cada fio retilíneo;
- Calcule o vetor força magnética que age sobre a parte circular;
- Calcule a força resultante que age sobre o fio todo;
Passo 1
- Calcule o vetor força magnética que age sobre cada fio retilíneo;
Beleza! Pra começar, vamos dividir esse cara em três partes, as duas retilíneas e a semicircular.
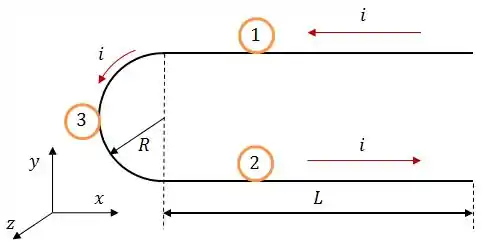
A força magnética sobre um fio é dada por:
Onde o segmento aponta sempre na direção da corrente.
Nesses casos, como se tratam de fios retilíneos:
- Fio 1:
- Fio 2:
Logo:
Portanto:
Passo 2
Pra termos uma ideia de pra onde está apontando vamos pegar um ponto aleatório do fio semicircular:
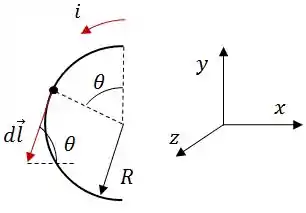
Podemos decompor o vetor nos eixos ortogonais como:
Como é o elemento infinitesimal desse arco, podemos escrevê-lo como:
Agora podemos calcular a força:
Passo 3
A força resultante será a soma vetorial das forças que já calculamos, logo:
Resposta
a.
b.
c.
Exercício Resolvido #7
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 27.39, pp. 235.
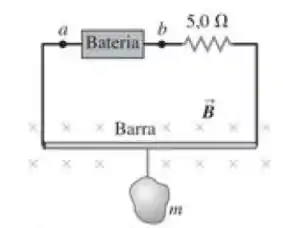
Uma barra metálica delgada, com de comprimento e massa , repousa sobre dois suportes metálicos (mas não está conectada a eles), em um campo magnético uniforme de , como indica a Figura abaixo. Uma bateria com ddp e um resistor de em série estão conectados aos suportes.
- Qual voltagem máxima a bateria pode ter sem romper o circuito nos suportes?
- A voltagem da bateria possui o valor máximo calculado no item (a). Supondo que o resistor repentinamente sofre um curto-circuito parcial, diminuindo sua resistência para , ache a aceleração inicial da barra.
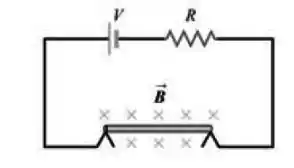
Passo 1
a) Aqui temos um típico problema de força em um condutor pelo qual passa corrente e que está na presença de um campo magnético. Quando esse condutor é percorrido por um corrente, ele sofre uma força que tem módulo dado
Bom, essa força precisa estar direcionada para cima para poder equilibrar o peso da barra. Portanto, o sentido da corrente deve ser anti-horário na Figura acima. Se a gente igual a força peso com a força magnética, chegamos a
Se uma corrente maior do que esse valor passar pela barra, então, a barra vai sentir uma força maior do que a força peso e vai ser acelerada para cima, que o caso que a gente vai ver no próximo item.
Continuando aqui, por enquanto, e colocando os valores dados no enunciado, o valor dessa corrente é
Então, a diferença de potencial é dada por
Passo 2
b) Se a ddp é a mesma que no caso do item (a), então a corrente agora vai ter o seguinte valor
que é bem maior do que a do caso anterior. Isso significa que a barra vai sofrer uma nova força magnética para cima maior do que o seu peso e, por isso, vai ser acelerada para cima. A aceleração que ele vai ter é
Colocando os valores da nova corrente e os do enunciado, a barra tem uma aceleração que é dada por
Resposta
Exercício Resolvido #8
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 27.40, pp. 235.
Balança magnética. O circuito da Figura abaixo é usado para produzir uma balança magnética para pesar objetos. A massa a ser medida está suspensa a partir do centro da barra, que se situa em um campo magnético uniforme de , orientado para dentro do plano da Figura. A voltagem da bateria pode ser ajustada de modo a variar a corrente no circuito. A barra condutora horizontal tem de comprimento e é feita de um material extremamente leve. Está conectada à bateria por fios verticais finos que não podem suportar nenhuma tensão considerável: todo o peso da massa suspensa é sustentado pela força magnética na barra. Um resistor de está ligado em série com a barra; a resistência do restante do circuito é muito menor que isso.
- Qual ponto, ou , deve ser o terminal positivo da bateria?
- Se a voltagem máxima do terminal da bateria é igual a , qual é a maior massa que esse instrumento pode medir?
Passo 1
a) Para esse dispositivo possa medir o valor do peso do objeto, é necessário que haja o equilíbrio entre a força peso e a força magnética que atuará na barra condutora pela qual passa uma corrente.
Como a força peso está direcionada para baixo, a força magnética deve estar para cima e precisa ter o módulo que a força peso. Por isso, aplicando a regra da mão direita, vemos que a corrente deve passar na barra no sentido da esquerda para a direita, ou seja, a corrente deve ter o sentido anti-horário.
Dessa maneira, o terminal deve ser positivo e o negativo.
Passo 2
b) Para ter esse valor máximo para a massa, a gente precisa igualar a força magnética com a força peso. Isso vai dar a seguinte expressão para a massa
Agora, a corrente que vai passar na barra é igual , em que é a ddp. Substituindo na expressão acima, temos
Resposta
- Corrente no sentido anti-horário, por isso o terminal é positivo e o terminal é negativo ;
Exercício Resolvido #9
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 27.67, pp. 238.
Um fio retilíneo condutor de massa e comprimento é colocado sobre um plano inclinado sem atrito, formando um ângulo com a horizontal, como mostra a Figura abaixo. Existe um campo magnético uniforme ao longo de todos os pontos (produzido por um conjunto de eletroímãs não indicados na Figura). Para impedir que o fio escorregue para baixo do plano, uma fonte de tensão é aplicada nas extremidades do fio. Quando uma corrente com um valor preciso circula no fio, ele permanece em repouso. Determine o módulo e o sentido da corrente que circula para fazer o fio ficar em repouso.
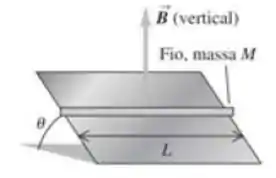
Passo 1
Bom, para que a barra condutora permaneça em repouso, é preciso que haja uma força que equilibre a compononte da força peso na direção do plano inclinado. A única maneira de haver uma componente da força magnética na mesma direção do plano inclinado e que possa equilibrar é que essa força seja como mostrada na Figura abaixo, apontando da direita para a esquerda e perpendicular à força peso.
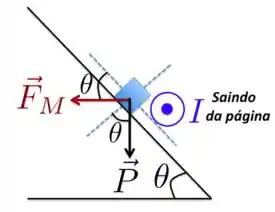
Para que a força magnética esteja como na Figura acima, a corrente que passa na barra condutora deve estar no sentido da direita para a esquerda se olhamos para a Figura do enunciado. Tranquilo? Isso a gente pode ver utilizando a regra da mão direita!!!
Passo 2
Agora que temos o sentido que a corrente deve ter, vamos igualar as forças
Então, esse é o valor que a corrente que passa na barra condutora deve ter para que fique em repouso. Se o ângulo aumenta, o valor dessa corrente também aumenta.
Por exemplo, se , ou seja, o plano perpendicular ao plano do chão, a corrente teria que ser para que a barra ficasse em repouso no plano.
Se , então, e, naturalmente, a barra vai ficar em repouso sobre o plano.
Resposta
A corrente deve percorrer a barra no sentido da direita para a esquerda e deve ter o valor
Exercício Resolvido #10
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 27.68, pp. 238.
Uma barra metálica de peso , com comprimento e resistência , respousa horizontalmente sobre fios condutores do circuito indicado na Figura abaixo. A barra está em um campo magnético horizontal uniforme de e não está conectada aos fios do condutor. Qual a aceleração da barra logo após a chave ser fechada?
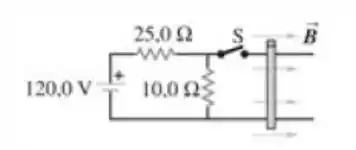
Passo 1
Vamos lá? Olha só, nesse exercício a gente tem um circuito ligado a uma bateria. A própria barra condutora tem uma resistência e, quando a chave é fechada, passa uma corrente por essa barra. Como ela em uma região onde tem campo magnético, passa a agir nela uma força magnética.
Como o sistema todo está na horizontal e o campo magnético está dirigido da esquerda para a direita, então vai aparecer uma força magnética para cima tirando a barra do circuito. Isso significa que deve passar uma corrente de cima para baixo na barra condutora. Para ver isso, basta a gente aplicar a regra da mão direita. Blz?
Precisamos descobrir que corrente é essa. Para isso, vamos ter que encontrar a resistência equivalente do circuito, considerando também a resistência de da barra condutora.
Passo 2
Bom, a resistência da barra está em paralelo com a resistência de e o resultado dessa associação está em série com o resistor de . Então, temos o seguinte
Com isso, descobrimos o valor da corrente que é
Essa é a corrente que passa também no resistor de .
Agora, a ddp entre as extremidades da barra condutora é
Portanto, a corrente que passa pela barra é
Passo 3
O próximo passo é calcular a força magnética que atua nessa barra. Como já temos o valor do campo magnético, que é perpendicular à barra, e também o comprimento da barra condutora, o valor da força é
A aceleração inicial da barra vai ser