Energia da Onda Eletromagnética
Produzido por Bruno SoaresTeoria
A energia de uma onda eletromagnética
As ondas eletromagnéticas fazem parte do nosso dia-a-dia! Estão por toda parte, e temos diversas aplicações para elas no nosso cotidiano.
Elas carregam energia, afinal de contas, transmissões de televisão, rádio, fornos micro-ondas, lâmpadas e etc., fazem uso da energia que as ondas eletromagnéticas transportam. (inclusive, existem carregadores de celular sem fio!!! )
O nosso trabalho aqui é conseguir entender como essa energia se comporta.
Densidade de energia
Densidade de energia (), por definição, é a energia () por unidade de volume (). Assim
A densidade de energia em uma região do espaço onde existe apenas um campo elétrico e um campo magnético é dada por
Onde é a permissividade no vácuo, que vale aproximadamente .
A constante representa a permeabilidade magnética no vácuo, que vale
Ok, quero te mostrar uma coisa nessa fórmula de densidade de energia. Mas antes, vamos relembrar algumas relações muito importantes que vamos utilizar.
Onde é a velocidade da luz no vácuo, que vale aproximadamente .
Agora sim, vamos lá!
Substituindo na fórmula de densidade de energia:
Isso nos mostra que a densidade de energia associada ao campo elétrico é igual à densidade de energia associada ao campo magnético .
Outra coisa que isso nos mostra é que, como o campo elétrico e o campo magnético variam em função do tempo e da posição ( e ), a densidade de energia também é uma função do tempo e da posição .
Densidade de energia
Exercícios Resolvidos
Exercício Resolvido #1
Young e Freedman, Física III Eletromagnetismo, 12ª ed, São Paulo: Addison Wesley, 2009, pp 402-32.41, modificado
Um pequeno laser de hélio-neônio emite luz vermelha cujas amplitudes do campo elétrico e do campo magnético são e concentrada em um feixe com diâmetro de .
- Calcule as densidades de energia médias associadas com o campo elétrico e com o campo magnético.
- Qual é a energia contida em um comprimento do feixe igual a ?
Passo 1
Letra
O problema nos pede para calcular as densidades de energia médias associadas com o campo elétrico e com o campo magnético.
A densidade de energia em uma região do espaço onde existe apenas um campo elétrico e um campo magnético é dada por
Vamos começar calculando a densidade de energia associada a , .
Onde:
;
;
Logo:
Quando falamos de densidade de energia, nós chegamos a uma conclusão importante, lembra?
Falamos nela que a densidade de energia associada a é igual à densidade de energia associada à , logo:
Passo 2
Letra
O problema nos pede para calcular a energia contida em um comprimento do feixe igual a .
Sabemos que a densidade de energia total é
Por definição, a densidade de energia é a energia por unidade de volume . Logo:
Podemos imaginar o feixe do laser como contido em um cilindro, e assim seu volume será:
Onde é o comprimento do cilindro e é a área da base. Pelo enunciado, o diâmetro do feixe é e assim seu raio será:
O que nos dá para seu volume:
Logo, a energia contida no feixe será:
Resposta
Letra
Letra
Exercício Resolvido #2
Elaboração própria
Mostre que na onda eletromagnética a densidade de energia elétrica é igual a magnética. Além disso, mostre que a densidade de energia total pode ser escrita em função de apenas uma das duas densidades de energia.
Passo 1
Vamos partir da densidade de energia elétrica, mas poderíamos partir da magnética também.
Temos que:
Substituindo na equação:
Mas:
Assim, a equacão fica:
Beleza, encontramos a densidade de energia magnética a partir da elétrica. Se partíssemos da magnética, isso também daria certo.
DICA: Se você quiser a prova disso, olhe o exercicío de trás para frente, a partir desse ponto.
Passo 2
Bom, agora a gente pode partir pra densidade de energia total. Como fizemos pela densidade de energia elétrica, vamos continuar com ela, ok?
A densidade de energia total é dada por:
Mas:
Então:
Para quem fez pela densidade de energia magnética:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria
Uma onda incide em uma superficíe quadrada. Sabendo que o módulo do campo elétrico dessa onda é , encontre a aresta do prisma representado abaixo e a intensidade da luz que emite essa onda, sabendo que a potência da fonte de luz é 2,39W.
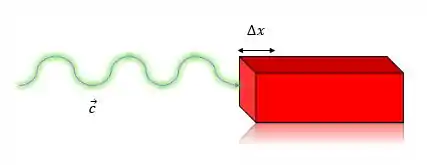
Passo 1
Precisamos encontrar a intensidade da fonte e a aresta, vamos começar com o volume que é dado por:
Onde é a área da seção transversal do prisma.
Podemos usar a densidade de energia elétrica para encontrarmos a densidade de energia total
já que temos o campo elétrico.
A densidade de energia total é inicialmente dada por:
Mas:
Se a densidade de energia é:
E a energia é:
A gente pode substituir e a fórmula vai ficar assim:
Passo 2
Com as duas equações da densidade, podemos igualá-las assim:
Relacionando potência e intensidade, conseguimos eliminar uma incógnita:
Voltando na equação, temos:
Mas:
Substituindo na equação e rearrumando, temos a intensidade:
Passo 3
Agora com a intensidade e a potência, a gente consegue encontrar a área de boa, lembrando que:
E como a área é quadrada, temos que:
Resposta
Exercício Resolvido #4
Elaboração própria
Prove as fórmulas das densidades de energia elétrica e magnética partindo da ideia mostrada na figura abaixo. A onda desloca o cilindro uma distância no sentido de propagação da mesma.
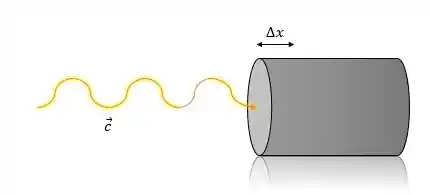
Passo 1
As densidades de energia são nada mais que energia por quantidade de volume. Observe que na figura, a onda desloca a distância a partir da face do cilindro. Assim, o volume que a energia preenche será:
Onde é a área da seção transversal do cilindro.
A densidade de energia é dada inicialmente por:
E a energia é:
Se a gente olhar a fórmula da intensidade, podemos relaciona-lá com a potência dessa forma:
A energia será então:
Passo 2
Vamos substituir o que encontramos na equação da densidade e ela vai ficar mais ou menos assim:
Como estamos trabalhando com uma onda eletromagnética, a velocidade é , então podemos dizer que:
Na equação temos o inverso disso, então o aparece embaixo e vai ficar assim:
Passo 3
Bom, a gente tem que chegar na densidade de energia magnética e agora só nos restou a intensidade pra mexer. Bora ver no que dá.
A fórmula da intensidade média diz que:
E se substituirmos na equação:
Vamos chegar nisso aqui:
Agora só precisamos usar a relação:
E a nossa equação vai ficar assim:
Passo 4
Para a densidade de energia elétrica, basta usarmos a relação:
E a densidade de energia magnética vai ficar:
Como:
Temos na equação: