Equação Diferencial da Onda
Produzido por Leonardo de BemTeoria
Introdução
Fala aí, você já deve ter ouvido falar em algum lugar que ondas se comportam dessa forma aqui certo?
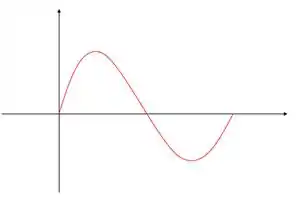
Até agora nós só tínhamos aprendido sobre ondas harmônicas, o nome pode ser novo mas são aquelas ondas descritas por senos e cossenos como essa aqui:
Mas e se eu te dissesse que podemos ter uma onda com uma configuração como essa aqui embaixo, você acreditaria?
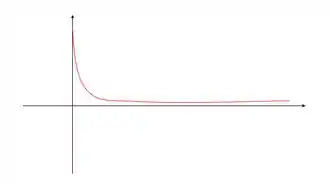

Pois é, esse gráfico bem doidão pode representar sim uma onda. A diferença é que nesse caso não seria uma onda harmônica descrita por um seno ou cosseno, mas sim por uma função diferente que no nosso caso é essa aqui:
Beleza, mas como podemos avaliar se isso é de fato uma onda?

Temos uma equação que vai ser fundamental na hora da gente avaliar isso, se liga:
Equação Diferencial da Onda
A equação, que é uma equação com derivadas parciais, é essa coisa linda aqui:
Onde é a velocidade da onda que também é conhecida como:
Onde é o comprimento da onda, é o período e é a frequência.
Nossa! Mas pra que isso serve?
Bom, é o seguinte: essa equação serve como uma “identidade” para as ondas. Ou seja, caso seja dito que uma determinada função descreve o comportamento de uma onda, essa função vai ter que satisfazer essa equação.
Huum, e como vamos “testar a identidade” de uma função dessas?
Vamos fazer um pequeno exemplo:
O movimento de uma onda harmônica qualquer é descrito por:
Rearranjando a equação da onda:
Vamos calcular cada uma das derivadas parciais da função e depois vamos jogar na relação acima:
E:
Agora usando a relação:
Lembrando que e :
E tirando a raíz:
Que é como se dá a velocidade da onda.
Sendo assim, concluímos que essa era realmente uma onda!
Se no final das contas, você encontrar algo diferente, provavelmente a função não descreve uma onda. MAS dê uma revisada nos seus cálculos, pois é comum cometer alguns errinhos aqui!
Esse teste pode ser aplicado a qualquer função que descreva uma onda, não precisa ser harmônica (ter seno ou cosseno).
Então se aplicarmos o teste na nossa equação daquele gráfico diferente poderíamos avaliar se ela descreve uma onda ou não:
Mas pra essa equação aí temos um outro método que pode ser bem interessante da gente avaliar, se liga!
Soluções da equação de onda (uma outra forma de se checar)
Beleza, então, se uma dada função representa uma onda, ela tem que satisfazer a equação diferencial de onda. Mas isso também equivale a dizer que a função é uma solução da equação diferencial de onda.
Show? O legal dessas soluções é que elas seguem um mesmo padrão, que é o:
Ou
Ou ainda, de forma mais geral, é uma combinação das duas:
E essa velocidade é aquela velocidade da onda mesmo:
Então você deve estar se perguntando: “Beleza, mas e aí?”
E aí que sabendo disso, você pode testar se uma dada equação representa uma onda sem usar a equação diferencial: basta que você chegue à conclusão que a função segue o padrão acima.
Vamos tentar aplicar o método na equação que vimos no começo e avaliar se é ou não uma onda, se liga:
Nosso foco aqui é o trecho que se parece com uma daquelas funções mostradas:
Vamos manipular ele um pouquinho:
Se ligou? O que tá dentro dos parênteses já tá bem parecido com o modelo que o método mostrou, mas pra essa equação ser de fato uma onda devemos ter a seguinte igualdade:
E aí parte dos parênteses fica com essa cara:
Bem parecida com essa função aqui:
Então temos uma onda aí caso .
Sacou? Isso vai te ajudar em algumas questões onde aplicar derivadas for muito difícil!
Partiu fazer uns exercícios?