Teoria
Olá, nós somos o Responde Aí, a plataforma de exatas criada para ajudar você a ter um bom aprendizado, de forma descontraída, e a mandar super bem na sua prova.
Nossa conversa hoje é sobre ondas. Partiu aprender ondas com o Responde Aí?
O que são Ondas?
Para entender o que são ondas, pensa em quando você joga uma pedrinha em um lago. Essa pedrinha quando cai na superfície causa uma perturbação, né?
Depois de um tempinho você percebe que aquela perturbação na superfície passou e a mesma quantidade de água que tinha antes no lago continua ali.
E é exatamente isso que a gente chama de onda: É uma pertubação que se propaga de um lugar para outro através de um meio (água nosse caso do lago) e transporta energia e não matéria.
Classificação da onda quanto a direção da propagação
As ondas podem ser classificadas em longitudinais ou tranversais de acordo com a direção que a perturbação se propaga.
- Ondas Longitudinais: As ondas longitudinais são aquelas em que a vibração se dá na mesma direção da propagação.
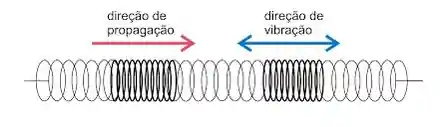
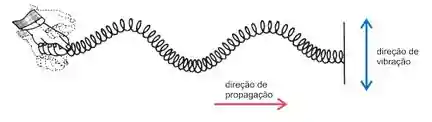
- Ondas Tranversais: As ondas transversais são aquelas que a vibração ocorre perpendicularmente a direção de propagação.
Natureza da Onda
Podemos ainda classificar as ondas em mecânicas e eletromagnéticas de acordo com o meio de propagação.
- Ondas mecânicas: Necessitam de um meio material para se propagar. Exemplo: som
- Ondas Eletromagnéticas: Não necessitam de um meio para se propagar, ou seja, se propagam também no vácuo. Exemplo: luz
É por isso que a luz do Sol consegue viajar lá de longe até você, mas não conseguimos ouvir nada que venha do espaço. Ou seja, aqueles sons das explosões de Star Wars são todos fake, já que no espaço não há matéria para o som se propagar. :(
Propriedades da Onda
Vamos imaginar agora que o macaquinho Dexter (ele é o mascote do Responde Aí hahaha) causou uma perturbação em uma corda gerando uma onda longitudinal:
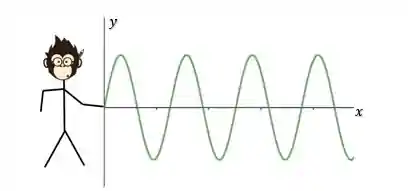
O ponto mais alto da onda é o que chamamos de crista e o ponto mais baixo é o que chamamos de vale:
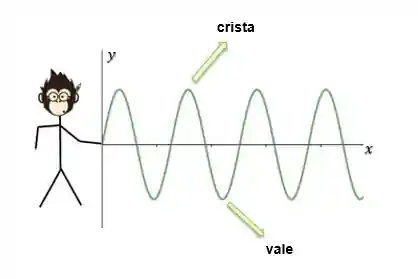
Podemos definir o que chamamos de comprimento de onda, representado pela letra grega lambda,
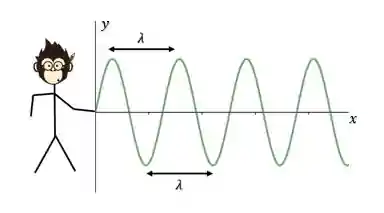
Definimos também a amplitude,
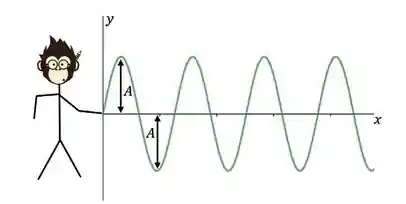
Outra parada muito importante é o período. O período é o tempo que a onda demora para se repetir, ou seja, o tempo que ela demora para percorrer um comprimento de onda, e é representado pela letra
Quando a onda se propaga, ela se propaga com uma velocidade constante, que chamamos de
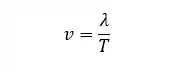
Outra coisa importante é a frequência, representada pela letra
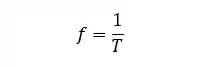
Sabendo disso, podemos reescrever a fórmula da velocidade em função do comprimento de onda e da frequência:
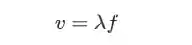
Essas são as principais coisas que você precisa saber sobre as ondas.
Se você quiser fixar ainda mais esses conceitos que aprendemos aqui hoje você pode assistir o vídeo que eu vou deixar aqui embaixo 👇🏾. Esse vídeo foi feito por nós do Responde Aí, com muita dedicação para você ter um aprendizado objetivo e eficaz.
Confere aí!
Vídeo
Confere aqui essa aula em vídeo sobre ondas 😉
Propriedades da Onda
Exercícios Resolvidos
Exercício Resolvido #1
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 16, pp 141-1
Uma onda possui frequência angular de rad/s e um comprimento de onda de m. Calcule:
- O número de onda;
- A velocidade de onda.
Passo 1
Para o item a, vamos aplicar a relação entre número de onda, comprimento de onda e frequência angular.
Passo 2
Para o item b, vamos aplicar a relação:
E:
Resposta
Exercício Resolvido #2
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 16, pp 141-3
Uma onda senoidal se propaga em uma corda. O tempo necessário para que um certo ponto da corda se mova do deslocamento máximo até zero é . Quais são:
- O período;
- A frequência da corda.
- O comprimento de onda é , qual é a velocidade da onda?
Passo 1
O período é o tempo que um elemento da corda leva para fazer uma oscilação completa, ou seja, retornar a sua posição original.
Logo, esse elemento se move do deslocamento máximo até zero, depois de zero até o deslocamento mínimo, do deslocamento mínimo até zero e finalmente, de zero até o deslocamento máximo.
Sendo assim, a primeira parte (se mover do deslocamento máximo até zero) corresponde a do ciclo. Tem-se:
Passo 2
Podemos relacionar frequência com período:
Passo 3
Relacionando velocidade com comprimento de onda e período:
Resposta
Exercício Resolvido #3
UFF – Lista de Exercícios de Ondas – Questão 42.
A figura é um gráfico-instantâneo, para , de uma onda de que se propaga para a esquerda.
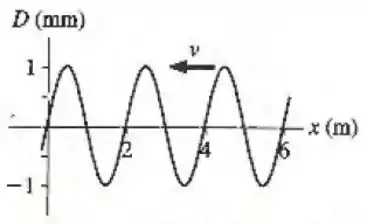
Qual é a velocidade da onda?
Qual é sua constante de fase?
Escreva a equação para os deslocamentos produzidos no meio por esta onda.
Passo 1
Bom, temos aqui um gráfico de para . Já sabemos como analisar esse gráfico.
Pelo gráfico, vemos que o comprimento de onda é .
Sendo a frequência , temos:
Passo 2
Para determinar a constante de fase, podemos analisar o gráfico. Vemos que para , temos que . Tendo em vista que é dado por:
Aqui você poderia ter usado cosseno ao invés de seno na expressão de . Se você fizesse isso, o resultado seria (testa só!)
Passo 3
Para determinar a equação da onda, vamos primeiro escrever a equação básica da onda e os valores que conhecemos:
Podemos extrair dos gráficos as seguintes informações:
A equação deve ficar assim:
Resposta
Exercício Resolvido #4
UFF – Lista de Exercícios de Ondas Harmônicas – Questão 13.
O deslocamento de uma onda que se propaga no sentido negativo do eixo é , onde está em , e em . Quais são:
A frequência.
O comprimento de onda.
A velocidade da onda.
Passo 1
Então, galera! Aqui temos uma equação de onda em e não em . Mas não se preocupe, é a mesma coisa (só trocar por )!
Vamos lá achar as informações pedidas, comparando com a nossa equação:
Passo 2
Olhando para a equação da onda, podemos extrair as seguintes informações:
Onde é a amplitude, é o número de onda e é a velocidade angular.
Para determinar a frequência, podemos utilizar a seguinte relação:
Passo 3
Para determinar o comprimento de onda, podemos usar a seguinte relação:
Passo 4
Para determinar a velocidade da onda, temos:
Substituindo, temos:
Resposta
Exercício Resolvido #5
PUC, Física 2, Prova 2, 2012.1 – a,b,c,d - Modificada
Uma onda transversal senoidal se propaga em uma corda no sentido negativo do eixo . A Figura abaixo mostra o deslocamento em função da posição no instante . A velocidade da onda é de . Assuma que a onda é da forma .
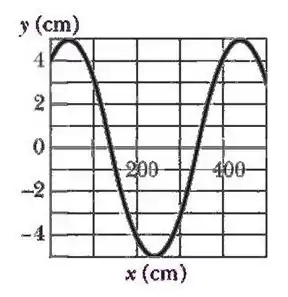
Determine a amplitude e o comprimento de onda.
Encontre o período e o sinal que precede .
Determine a velocidade transversal máxima de uma partícula da corda.
Determine a constante de fase .
Passo 1
Analisando o gráfico, podemos ver que a distância do eixo até um ponto de máximo, ou seja, a amplitude é:
O comprimento de onda, a distância entre dois pontos de máximo, é:
Passo 2
Para calcular a período, podemos usar a seguinte relação:
Como ele diz que a onda se propaga no sentido negativo, temos que o sinal que precede deve ser positivo .
Passo 3
Para determinar a velocidade máxima, devemos calcular a primeira derivada em relação ao tempo da função :
A velocidade será máxima quando for igual a , quando isso ocorrer, temos:
Passo 4
Para determinar a constante de fase, devemos utilizar a função , pois sabemos do gráfico que .
Na equação, temos:
Resposta
;
;
O sinal que precede é positivo .
Exercício Resolvido #6
PUC, Física 2, Prova 2, 2011.1 – letras a,b
- Escreva, literalmente, a expressão de uma onda harmônica progressiva unidimensional, propagando-se no sentido positivo do eixo x, em termos da amplitude , da frequência e do comprimento de onda .
- A partir dessa expressão, determine a velocidade máxima com que um elemento do meio se movimenta.
Passo 1
a)
A expressão é:
Sabemos que:
( Número de onda)
(frequência angular)
Fase inicial.
Podemos escrever essa expressão assim também:
Passo 2
b)
Bom, a velocidade máxima vai ser a máxima taxa de variação de . Logo, vai ser o máximo de:
Essa é a chamada velocidade transversal de uma onda. Essa expressão tem um máximo quando a parte do cosseno se iguala à 1. Com isso igualado à 1, fica:
Resposta
a)
b)
Exercício Resolvido #7
PUC, Física 2, Prova 2, 2014.2 – Questão 1
Uma onda senoidal se propaga ao longo de uma corda sob tensão. A figura 1 fornece a inclinação da corda ao longo do eixo no instante . Suponha que a equação da onda progressiva é do tipo
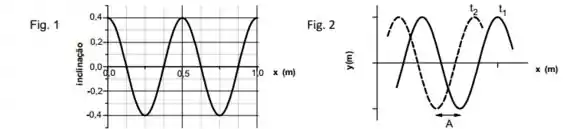
- Calcule a amplitude da onda progressiva.
- Calcule a constante de fase.
- Calcule a frequência da onda progressiva.
- Escreva a equação , com os valores pra , e , e com o sinal correto em frente a , baseando-se na análise das figuras 1 e 2.
A figura 2 mostra dois instantes diferentes de um pedaço da mesma onda progressiva da figura 1. Na figura , e
Passo 1
a)
Bom, sabemos que a função de uma onda harmônica é do tipo:
Então:
Sabemos que essa derivada tem um máximo quando:
E pelo gráfico:
Passo 2
Outra informação que podemos tirar do gráfico é acerca do comprimento de onda. Pelo gráfico, vemos que os picos se repetem a cada . Isso quer dizer que a cada a onda completa um ciclo, o que quer dizer que:
E como:
Então:
Passo 3
b)
A função da derivada nos dá:
Substituindo e :
Só que sabemos que nesse ponto temos:
Logo:
Passo 4
c)
Bom, o caminho pra se calcular a frequência passa por calcular a velocidade:
Então:
Passo 5
d)
A equação segue o padrão:
E:
Então, lembrando de todas as variáveis que calculamos:
Resposta
a)
b)
c)
d)
Exercício Resolvido #8
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 16, pp 142-6
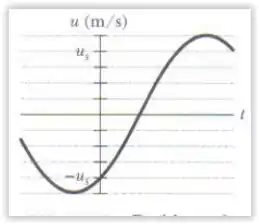
A figura abaixo mostra a velocidade transversal em função do tempo para o ponto de uma corda situado em , quando uma onda passa por ele. A escala do eixo vertical é definida por . A onda tem a forma . Qual é o valor de ?
Passo 1
Sendo
Podemos dizer que
Como para o gráfico mostrado, , então:
Passo 2
Analisando a equação, vemos que:
Pois:
No gráfico,
Passo 3
Pelo gráfico, podemos ver também que quando , .
Logo:
ou
Passo 4
Para descobrirmos qual é o valor certo vamos derivar a função do gráfico
Pelo gráfico, vemos que no ponto , a função é crescente. Então, a derivada é maior que zero.
Logo,
Se o seno é menor que zero, o ângulo é do terceiro ou quarto quadrante. Logo:
É importante lembrar que quando acrescentamos , sendo n qualquer número inteiro, o ângulo também é válido como resposta.
Resposta
Exercício Resolvido #9
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 16, pp 146-64
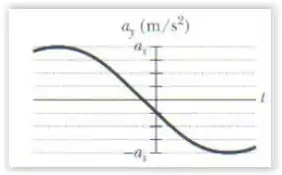
A figura abaixo mostra a aceleração transversal em função do tempo do ponto de uma corda, quando uma onda com a forma geral passa pelo ponto. A escala do eixo vertical é definida por . Qual é o valor de ?
Passo 1
Sendo:
Podemos dizer que:
Derivando mais uma vez para acharmos a aceleração transversal chegamos a:
Passo 2
Como :
Já que seno varia de até :
=
Pelo gráfico da figura, .
Passo 3
Pelo gráfico podemos ver também que quando , .
Logo:
ou
ou
Passo 4
Pra saber qual o valor correto da constante de fase, podemos fazer:
Como essa derivada acima é igual a inclinação da tangente na curva, no ponto , temos que a curva é decrescente, logo:
Assim:
É importante lembrar que quando acrescentamos , sendo n qualquer número inteiro, o ângulo também é válido como resposta.
Resposta
Exercício Resolvido #10
PUC, Física 2, Prova 2, 2011.1 – letras a,b
A função de onda para uma onda progressiva em uma corda esticada é (em unidades do SI):
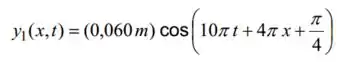
Suponha que a corda possui uma massa por unidade de comprimento de
- Obtenha o comprimento de onda, a velocidade e o sentido de propagação da onda.
- Obtenha o valor máximo de velocidade transversal da corda. Para a posição , em que instantes esse valor máximo ocorre? (Dê os dois primeiros, para
Passo 1
a)
Aqui, vamos identificar as variáveis que queremos comparando com a equação geral da onda:
Lembrando que:
Então:
E:
E o sentido da propagação é negativo, já que estamos somando a frequência angular e não subtraindo.
Passo 2
Falta ainda calcular a velocidade de propagação.
Usando a relação:
Passo 3
b)
Lembra como a gente calcula a velocidade transversal? É a derivada parcial daquela função lá de cima em relação ao tempo:
Para
Passo 4
Quando a velocidade terá um máximo?
Se o que queremos é o maior valor positivo, vai ser quando o “ângulo” do seno for igual a , para que o seno seja igual a . Assim:
E esse é o tempo para o qual temos a velocidade máxima.
Quando o seno for igual a :
E o segundo valor? Basta a gente acrescentar a mais em
Resposta
a)
Sentido negativo.
b)