Difração por uma Fenda Circular

Teoria

Difração por orifício circular

Quando a luz incide num buraco redondo, o fenômeno de difração muda um pouco.

No caso das fendas retangulares, tínhamos várias franjas paralelas.

Agora, para orifícios circulares como por exemplo, as lentes de uma câmera fotográfica, teremos vários anéis claros e escuros circundando um disco central, que é chamado disco de Airy.

E não podemos usar o mesmo procedimento para achar os mínimos de difração nesse caso. E agora, quem poderá nos ajudar?

Não tema! Ainda podemos encontrar o primeiro mínimo de difração se consertarmos ligeiramente a fórmula da difração por fenda simples.

Se o diâmetro do orifício é e o comprimento de onda é , o desvio angular do primeiro anel escuro em relação ao centro do círculo é dado por:

Isso só vale para o primeiro mínimo!

(Note que, na fenda simples, tínhamos , onde era a largura da abertura. Ou seja, só consertamos a fórmula por um fator de )

Lembrando-se da aproximação de pequenos ângulos, também podemos dizer que:

E também, se a distância até o anteparo é , e o raio do primeiro anel escuro é , temos a situação da figura abaixo

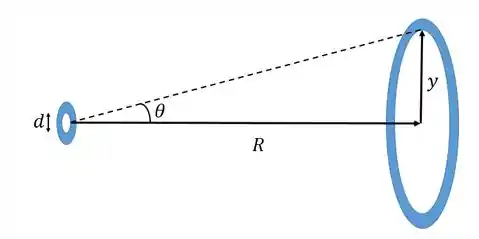
A tangente de é dada por

Na aproximação de ângulos pequenos temos que . Assim

Encontrar a posição dos mínimos seguintes não é tão simples, e em geral também não costuma ser importante.

Além disso, o gráfico de intensidade tem a forma muito parecida com o da difração por fenda simples.

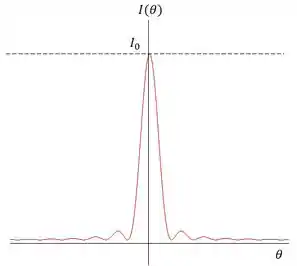
Com a diferença que os pontos dos máximos e dos mínimos são diferentes.

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 139-22

Halos entópticos. Quando uma pessoa olha para uma lâmpada de rua em uma noite escura a lâmpada parece estar cercada de anéis claros e escuros (daí o nome halos), que são na verdade uma figura de difração circular como a da Fig.36-10, com o máximo central coincidindo com a luz direta da lâmpada.

A difração é produzida por estruturas da córnea ou do cristalino do olho (daí o nome entópticos).

Se a lâmpada é monocromática, com um comprimento de onda de , e o primeiro anel escuro subentende um diâmetro angular de do ponto de vista do observador, qual é o diâmetro (linear) da estrutura que produz a figura de difração?

Passo 1

A condição para o primeiro mínimo de difração no caso de aberturas circulares é:

O ângulo é o ângulo entre o centro da figura de difração e o primeiro anel escuro.

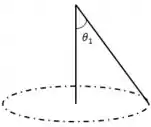
O problema nos diz que o diâmetro angular do primeiro anel escuro é que é o ângulo entre dois pontos diametralmente opostos do anel. Por isso:

Além disso, é o comprimento de onda da luz incidente e é o diâmetro da abertura circular que produz a figura de difração.

Passo 2

Rearranjando a equação do primeiro mínimo:

Substituindo os valores dados:

Resposta

O diâmetro da estrutura que produz a figura de difração é .

Exercício Resolvido #2

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 139-29, modificado

Os aparelhos de radar de ondas milimétricas produzem um feixe mais estreito que os aparelhos de radar convencionais de micro-ondas, o que os torna menos vulneráveis aos mísseis anti-radar.

Calcule a largura angular do máximo central, do primeiro mínimo de um lado ao primeiro mínimo do outro, para um radar de com uma antena circular com de diâmetro. (A frequência foi escolhida para coincidir com uma “janela” atmosférica de baixa absorção.)
Qual é o valor de para uma antena circular convencional, com de diâmetro, que trabalha com um comprimento de onda de ?