Poder de Resolução e Critério de Rayleigh
Teoria
O que é poder de resolução?
Quem já viu uma imagem feita de vários pontinhos, que quando você olhava de longe, parecia uma imagem normal? Existia um tipo de arte, chamado “pontilhismo” que era assim!
Nunca viu uma pintura do pontilhismo? Bem, ainda assim com certeza você já viu uma imagem que era assim, afinal, você tá lendo esse resumo no seu computador. O monitor do seu computador é feito de vários pontos que chamamos “pixels”, que estão tão pertos um do outro, que não conseguimos distinguir um do outro.
O quanto podemos distinguir dois pontos próximos é o que chamamos de poder de resolução do olho.
O poder de resolução é dado pelo critério de Rayleigh
Mas afinal, qual o poder de resolução do olho humano? Como sequer podemos saber isso?
Imagina que seu olho é como uma fenda. Quando a luz que vem de um objeto passar por ele, ela vai difratar, fazendo uma figura de difração na sua retina! Vamos observar duas figuras de difração de dois pixels diferentes.
Quando os dois estão muito pertos, temos dificuldade em ver os dois pixels. A medida que eles vão se afastando, vai ficando mais fácil distinguir entre eles. Vamos deixar um pixel vermelho, o outro verde, e ver as figuras de difração deles enquanto eles se afastam.
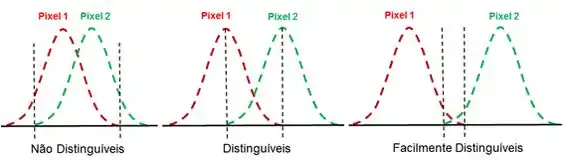
Quando os picos de difração são muito próximos, não conseguimos dizer que são dois picos, invés de um. Mas chega uma hora que podemos distinguir os dois com certa confiança. Isso é dado pelo que chamamos de critério de Rayleigh.
Quando a distância dos dois objetos for maior que essa eles são fáceis de serem distinguidos! Vamos tentar ver as fórmulas.
Como seu olho é redondo, a gente pode considerar ele como uma abertura circular! Além disso, podemos considerar que os ângulos envolvidos são pequenos. Juntando os dois, o menor ângulo necessário para você distinguir dois pixels do computador é dado por:
Se o ângulo entre eles for maior que esse, você vai conseguir ver dois objetos facilmente, invés de uma só imagem difusa.
Agora, vamos tentar ver a distância entre esses dois pontos.
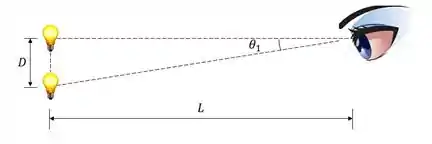
Como estamos em ângulos pequenos, também temos que . Assim:
O poder de resolução é dado pelo critério de Rayleigh
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 139-21
Os dois faróis de um automóvel que se aproxima de um observador estão separados por uma distância de . Qual é:
- A separação angula mínima?
- A distância mínima para que o olho do observador seja capaz de resolvê-los?
Suponha que o diâmetro da pupila do observador é e use um comprimento de onda da luz de para a luz dos faróis.
Suponha também que a resolução é limitada apenas pelos efeitos da difração e, portanto, que o critério de Rayleigh pode ser aplicado.
Passo 1
Letra a)
A separação angular mínima para o olho humano distinguir os dois faróis vai ser aquela na qual o mínimo de difração de cada farol coincide com o máximo do outro.
Vamos avaliar para um dos faróis:
Onde é o diâmetro da pupila do observador e é o comprimento de onda da luz do farol. Resolvendo:
O que nos mostra que poderíamos ter usado a aproximação de pequenos ângulos diretamente e feito .
Passo 2
Letra b)
Com o ângulo encontrado, podemos encontrar a distância mínima entre o olho e os faróis a partir da tangente do ângulo.
Pelo gráfico vemos que:
Que nos permite encontrar a distância mínima à qual o olho deve estar dos faróis para distinguí-los, usando a distância entre eles .
Rearranjando:
Resposta
Letra (a)
Letra (b)
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 143-76
Um astronauta a bordo de um ônibus espacial afirma que pode resolver com dificuldade dois pontos sobre a superfície da Terra, abaixo. Calcule:
- A separação angular dos pontos
- A separação linear dos pontos
Suponha condições ideais. Tome como o comprimento de onda da luz e como o diâmetro da pupila do astronauta.
Passo 1
Letra a)
A separação angular mínima para o astronauta resolver dois pontos com dificuldade é, usando a aproximação de pequenos ângulos:
O comprimento de onda da luz é e o diâmetro da pupila é . Substituindo:
Que é a separação angular dos dois pontos.
Passo 2
Letra b)
Para acharmos a separação linear entre os pontos, já tendo o ângulo entre eles, podemos usar a tangente do ângulo.
Onde é a separação linear dos pontos e é a distância do astronauta até os pontos na Terra.
Substituindo:
Resposta
Letra (a)
Letra (b)
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 144-90
A pupila do olho de uma pessoa tem um diâmetro de . De acordo com o critério de Rayleigh, qual deve ser a distância entre dois pequenos objetos para que estejam no limite da resolução quando se encontram a de distância do olho?
Suponha que o comprimento de onda da luz é .
Passo 1
Vamos resolver este exercício de duas maneiras para poder compará-las.
Primeiro, consideremos que os ângulos envolvidos são muito pequenos. Assim, para encontrar a distância entre os dois pequenos objetos podemos usar direto a equação:
Onde é o comprimento de onda da luz, é o diâmetro da pupila da pessoa e é a distância dos objetos ao olho da pessoa.
A distância necessária entre os dois pequenos objetos para que estejam no limite da resolução vai ser:
Passo 2
Agora, vamos evitar a consideração de pequenos ângulos.
Dessa forma, vamos primeiro precisar descobrir o menor ângulo entre os dois objetos para depois encontrar a distância entre eles.
Para o ângulo:
O que já nos comprova que nossa aproximação de pequenos ângulos é suficientemente boa.
Passo 3
Para terminar, nós encontramos a distância entre os dois objetos pela tangente do ângulo.
Que é a mesma resposta que tínhamos encontrado antes.
Os dois caminhos são possíveis e têm suas vantagens, então você pode escolher o que você achar melhor.
O primeiro é mais rápido, mas é uma fórmula pronta, com a explicação embutida.
O segundo demora mais, mas você vai montando a fórmula e entendendo cada etapa (inclusive o problema pode pedir essas etapas em vários itens).