Filmes Finos em Forma de Cunha
Teoria
Filmes Finos podem formar franjas de interferência?
Em um filme fino, o raio de luz que é refletido no topo do filme fino e o raio de luz refletido no fundo do filme fino interferem entre si. Porém, isso não forma várias franjas de interferência como no experimento de dupla fenda.
Prova disso é o insulfilm do carro, que é completamente escuro.
Mas se olharmos, por exemplo, um filme de sabão, ele tem várias franjas em várias cores ao longo dele!
Como é possível ter essas franjas?
A resposta: um filme fino com espessura variável!
Quando a espessura de um filme fino varia, nós podemos ter ao longo dele máximos e mínimos de interferência intercalados, formando franjas de interferência.
Variando a espessura...
Vamos primeiro montar um filme fino cuja espessura vai mudando ao longo dele. Pra isso, vamos juntar dois pedaços de vidro, e colocar uma borrachinha em uma das pontas
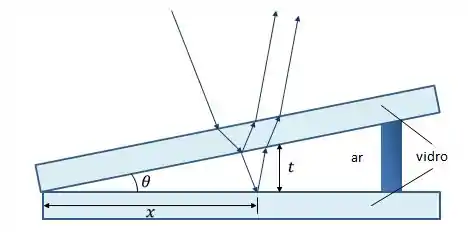
E voilà, temos um filme fino de ar entre os dois pedaços!
Como temos ar com dois pedaços de vidro em volta, apenas o raio que é refletido no fundo do filme de ar sofrerá mudança de fase por reflexão. (No caso mais geral, onde qualquer um dos dois puder mudar de fase, os conceitos serão os mesmos, só as equações que mudarão um pouco.)
Neste caso, a condição de interferência construtiva é:
Onde é a espessura do filme. Rearranjando a equação, vemos uma relação direta da espessura com a ordem dos máximos:
A medida que a espessura do filme aumenta, temos máximos de ordens cada vez mais altas.
O mesmo vale para os mínimos de interferência:
Em geral, as questões costumam de alguma forma misturar essas fórmulas com a geometria do problema. Então é importante lembrar da tangente do ângulo:
Para fixar a idéia, vamos ver um exemplo.
Vamos considerar que a nossa cunha tem de comprimento e a espessura da borrachinha é de e uma luz com comprimento de onda incide sobre ela.
Qual a posição da terceira franja escura ao longo da largura do filme de ar?
Usando as condições de interferência destrutiva, temos para a terceira franja escura:
Agora precisamos achar a espessura nessa terceira franja.
Como o filme é feito de ar, e assim temos:
Queremos encontrar o ponto no qual a espessura da cunha é de .
Sejam a espessura do filme na borrachinha e a largura do filme.
Vemos pela figura acima que:
A posição em é:
Passando tudo para milímetros e substituindo, temos:
Poderíamos repetir uma pergunta assim para diferentes franjas (escuras ou claras) ou pedindo o valor de outras coisas (o ângulo entre as cunhas, a variação da espessura ao longo das cunhas, etc...)
Obs:
Cuidado! Lembre que as equações mudam dependendo de quais reflexões (no topo e/ou no fundo) causam mudança de fase.
Obs2:
Nos exercícios, você não precisa se preocupar com considerações em relação ao ângulo que a luz atinge o filme fino. Vamos considerar sempre que é perpendicular e que a ligeira inclinação do filme não atrapalha nossa aproximação.
Variando a espessura...
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 109-113.
Na Fig.35-46, duas placas de vidro () formam uma cunha, e um fluido () é usado para preencher o espaço entre as placas. Do lado esquerdo as placas se tocam: do lado direito estão separadas por uma distância de .
Uma luz com um comprimento de onda (no ar) de incide perpendicularmente na placa superior, e um observador situado acima das placas vê a figura de interferência resultante.
- Existe uma franja clara ou escura na extremidade esquerda das placas?
- Existe uma franja clara ou escura na extremidade direita das placas?
- Quantas franjas escuras são observadas?
Passo 1
a)
Na extremidade esquerda, o filme tem espessura muito próxima de zero.
Nesse caso, teremos uma franja escura, que corresponde a na condição de mínimo de interferência em filmes finos.
Passo 2
b)
Na extremidade direita, a espessura do filme é de .
Como o fluido no meio das placas ainda tem um índice de refração menor que o das placas, as condições de máximo e mínimo de interferência vão continuar sendo as mesmas que as usadas quando tínhamos ar no meio das placas.
Interferência construtiva:
Interferência destrutiva:
E para ambos:
Dado que o índice de refração do filme é e o comprimento de onda da luz é de , teremos para uma possível ordem de máximo ou mínimo de interferência:
Que é um número inteiro, o que indica que na extremidade direita temos uma franja escura.
Passo 3
c)
Sabemos que a franja na extremidade esquerda é escura e a na extremidade direita também.
Além disso, a franja escura da extremidade direita é de ordem . Isso significa que temos 4 franjas escuras ao longo da cunha (de ordens , , e ).
Resposta
a)
Na extremidade esquerda das placas a franja é escura.
b)
Na extremidade direita das placas a franja é escura.
c)
São observadas 4 franjas escuras.
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 105-70.
Duas placas retangulares de vidro () estão em contato em uma das extremidades e separadas na outra extremidade (Fig.35-46). Um feixe de luz com um comprimento de onda de incide perpendicularmente à placa superior. O ar entre as placas se comporta como um filme fino.
Um observador que olha para baixo através da placa superior vê nove franjas escuras e oito franjas claras.
Quantas franjas escuras são vistas se a distância máxima entre as placas aumenta ?
Passo 1
Como o observador vê uma franja escura a mais que as franjas claras, então deve ser o caso que temos uma franja escura em cada borda do filme fino.
Isso significa que para a distância máxima entre as placas, vale a condição de interferência destrutiva, que no caso (ar envolta de placas de vidro) é:
Como o filme é ar, temos
Passo 2
Lembrando que temos franjas escuras, essa franja é a de ordem , pois a contagem começa com . O comprimento de onda da luz é
A espessura nesse ponto é:
Passo 3
Se aumentarmos a distância máxima das placas em , ela vai passar a ser:
Se substituirmos isso na condição de interferência, acharemos um mínimo de nova ordem:
Ou seja, o novo mínimo é de ordem , o que nos diz que agora temos mínimos de interferência.
Resposta
Veremos franjas escuras para a nova distância.
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 105-73.
Na Fig.35-46, duas lâminas de microscópio estão em contato em uma das extremidades e separadas na outra.
Quando uma luz com um comprimento de onda de incide verticalmente na lâmina superior, um observador situado acima das lâminas vê uma figura de interferência na qual as franjas escuras estão separadas por uma distância de .
Qual é o ângulo entre as lâminas?
Passo 1
Vamos tentar encontrar a distância entre duas franjas escuras.
A condição para mínimo de interferência é:
Como o filme é ar:
Para a franja escura seguinte, a espessura será:
A diferença de espessuras será:
O enunciado nos diz que , e substituindo:
Passo 2
Agora olhemos a geometria do problema:
Temos a distância entre duas franjas dadas pelo problema, e a diferença entre as alturas (espessuras), .
Podemos encontrar o ângulo pela sua tangente:
Resposta
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 105-75, modificado.
A Fig.35-47a mostra uma lente com raio de curvatura pousada em uma placa de vidro e iluminada de cima por uma luz de comprimento de onda .
A Fig.35-47b (uma fotografia tirada de um ponto acima da lente) revela a existência de franjas de interferência circulares (os chamados anéis de Newton) associadas à espessura variável do filme de ar que existe entre a lente e a placa.
Determine os raios dos anéis que correspondem aos máximos de interferência, supondo que .
Passo 1
O raio do anel é dado por . Pela figura, vemos que para um ponto do filme fino de espessura , forma-se um triângulo retângulo de lados , e .
Este último é porque a lente é esférica: a distância do centro de curvatura até o centro da lente será .
Como é um triângulo retângulo, podemos usar a equação de Pitágoras:
O problema nos diz que a espessura do filme fino é muito menor do que o raio de curvatura, ou seja:
Se dividirmos nossa equação por :
Como , nós podemos desprezar o segundo termo da equação, e obter:
Passo 2
Sendo a espessura do filme de ar (e, sendo um filme de ar, consideramos que que é menor que o da placa e o da lente), a condição para os máximos de interferência será:
O que nos permite encontrar a espessura com base na ordem do máximo.
Se substituirmos esse valor na equação anterior: