Interferência com Múltiplas Fendas Pontuais
Teoria
O que muda para um sistema de muitas fendas?
Ok, hora de pegar pesado. Vamos apontar nosso laser não para duas fendas, mas sim para um CD.
O CD é composto de vários sulcos que codificam a informação que tem nele. Esses sulcos são equivalentes a fendas estreitas, todas separadas por uma mesma distância entre elas.
Como ficaria o nosso experimento nesse caso? ( Sabe essas cores no CD? Assim como as das bolhas de sabão, elas são resultado do fenômeno de interferência )
Primeiramente, a diferença de fase entre as ondas de duas fendas consecutivas será sempre:
Logo, a diferença entre a 1ª onda e a 3ª onda será , entre a 1ª e a 4ª será , e assim por diante. A intensidade resultante dessa interferência com fontes luminosas vai ser:
Onde é a intensidade da luz incidente.
É muito mais jogo você entender os gráficos de intensidade do que simplesmente decorar essa fórmula. Então aqui vão algumas dicas que vão ajudar bastante, ok?
Eu coloquei 3 gráficos aqui embaixo, onde é o número de fendas ao qual o gráfico corresponde.
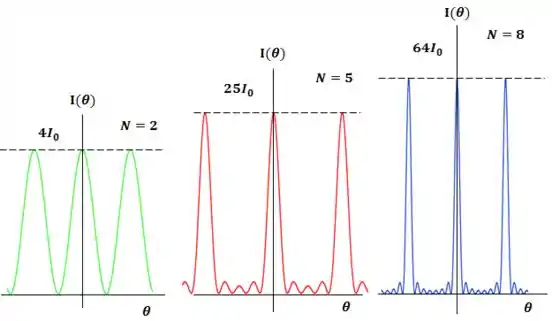
Os máximos maiores para qualquer número de fendas estão localizados nas mesmas posições do caso de fenda dupla.
Chamamos esses máximos maiores de máximos principais e aos máximos menores, localizados entre dois máximos principais, damos o nome de máximos secundários.
Observando os gráficos, podemos ver que (dá uma olhadinha ali em cima):
Cada um desses mínimos ocorre quando:
Ou seja, quando a diferença de fase entre duas fontes de ondas adjacentes for igual a um múltiplo inteiro de , desde que não seja múltiplo de (que corresponde a um máximo principal).
Tem outras duas informações muito importantes que podemos tirar dos gráficos:
E por hoje é só! Não esqueça de conferir os exercícios na saída!
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ, Física 4, Prova 1, 2009.1
Em uma demonstração de interferência com ondas sonoras, cinco alto-falantes emitem ondas de frequência igual a e intensidade .
Os alto-falantes estão em fase e separados entre si por uma distância de . A disposição geométrica dos alto-falantes é mostrada na figura abaixo.
As medidas da intensidade do som são feitas por um experimentador que se posiciona sobre a reta , a do plano que contém os alto-falantes. A velocidade do som no ar nas CNTP é de .
Considere os alto-falantes como fontes puntiformes, e despreze efeitos de reflexão nas paredes do laboratório.
- Calcule o valor máximo da razão , onde é a intensidade de um alto-falante.
- Calcule a distância linear sobre a reta de observação entre o máximo central e um máximo principal de primeira ordem.
- Quantos zeros há entre dois máximos principais consecutivos?
- Faça o diagrama de fasores correspondente ao primeiro mínimo.
Passo 1
a) Calcule o valor máximo da razão , onde é a intensidade de um alto-falante.
Para múltiplas fendas, a interferência é dada por:
Onde é o número de fendas que no nosso caso é o número de alto-falantes.
Uma das informações importantes que podemos tirar dos gráficos é que a altura de cada máximo principal é proporcional a .
Como temos 5 fendas, o gráfico da interferência é algo desse tipo:
Assim, o maior valor possível da fração será referente ao maior valor possível de , que, no caso de 5 fendas, será:
Logo:
Passo 2
b) Calcule a distância linear sobre a reta de observação entre o máximo central e um máximo principal de primeira ordem.
O problema nos pede a distância linear sobre a reta de observação .
Os máximos maiores estão localizados nas mesmas posições do caso de fenda dupla.
Logo, a posição dos máximos, medida a partir do máximo central é dada por:
Onde:
;
;
Como o problema está falando do máximo principal de primeira ordem,
Nos falta apenas descobrir o valor de .
Passo 3
Como o problema nos dá a frequência e a velocidade da onda, para descobrir o valor do comprimento de onda , podemos usar a seguinte relação:
Onde:
;
;
Logo:
Passo 4
Passo 5
c) Quantos zeros há entre dois máximos principais consecutivos?
Para fendas, outra informação muito importante que podemos tirar dos gráficos é que entre dois máximos principais existem máximos secundários e mínimos, respondendo a nossa pergunta.
Assim, existem zeros entre dois máximos principais.
Passo 6
d) Faça o diagrama de fasores correspondente ao primeiro mínimo.
Cada um dos mínimos ocorre quando a diferença de fase entre duas ondas consecutivas é dada por:
Como estamos falando do primeiro mínimo, a diferença de fase é dada por:
Passo 7
Como se tratam de 5 fendas, o diagrama de fasores será desta forma.
Lembrando que, ao somar a diferença de fase cinco vezes resulta , um círculo completo. Por isso, terminamos onde começamos.
Resposta
a)
b)
c)
Existem 4 zeros entre dois máximos principais.
d)
