Degrau e Tunelamento
Produzido por Bruno SoaresTeoria
Imagine a seguinte situação.
Eu pego um carrinho de brinquedo e empurro-o, o fazendo subir uma ladeira com o empurrão que eu dei. Ele vai subir até certo ponto, e depois descer de novo.
O que acontece é que a medida que ele vai subindo, a sua energia cinética vai virando energia potencial gravitacional. O ponto onde ele para é o ponto onde toda a energia que demos pra ele virou potencial. Ele não consegue subir acima disso.
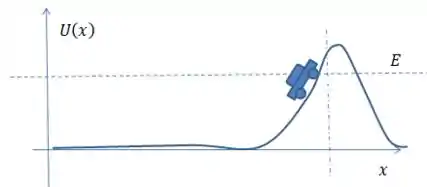
Se invés de uma ladeira, eu tivesse uma parede, ele nem subiria nada. Ele bateria na parede, e voltaria pra trás.
Na quântica, quando jogamos a partícula numa ladeira dessas, algo bizarro acontece: A partícula tem uma probabilidade de entrar na barreira de potencial e aparecer do outro lado.
O degrau quântico
Chamamos de “degrau quântico” ou “degrau de potencial” quando o gráfico de tem uma subida ou descida que, da nossa visão, assemelha-se a um degrau no caminho da partícula.
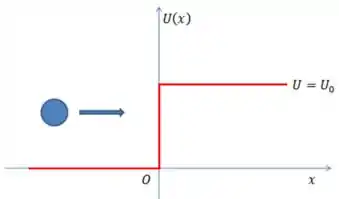
Quando existe apenas um degrau e ele logo desce, ou seja, volta ao estado inicial, a partícula encontra uma barreira, por isso é chamada “barreira de potencial”.
Vamos montar o problema: Uma partícula seguindo em direção a uma barreira de potencial.
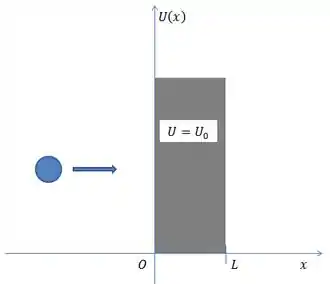
Considerando que a energia da partícula é menor que a barreira de potencial: .
Dos lados de fora da barreira, o potencial é zero e a equação de Schrödinger fica:
Onde:
Cuja solução, por causa do sinal negativo, é uma combinação de senos e cossenos.
Dentro da barreira, temos , e por isso a equação de Schrödinger fica:
Onde:
Por causa do sinal positivo, a solução vai ser uma combinação de exponenciais.
Agora é que surge a bizarrice:
Dentro da barreira, a função vai ser uma exponencial decrescente e não necessariamente zero. Isso vai fazer com que, dependendo da largura da barreira, seja suficientemente maior que zero para que vire o seno e cosseno do lado de fora.
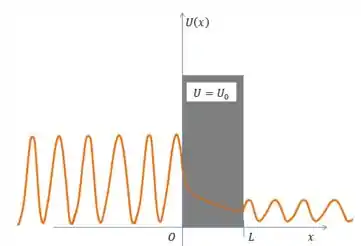
E por isso, quando várias partículas baterem na barreira, algumas vão conseguir atravessá-la!
O nome desse fenômeno é tunelamento, e de vez em quando você pode ouvir alguém dizendo que as partículas que atravessaram a barreira tunelaram.
A função de onda nos diz a probabilidade de encontrarmos a partícula em certos lugares, e não a certeza de que uma partícula se enfiou dentro de uma ladeira.
Por isso nós dizemos que a partícula tem certa probabilidade de tunelar pela barreira. De fato, é possível até calcular essa probabilidade.
Essa probabilidade será:
Onde é a largura da barreira e (assim como antes)
Também podemos escrever:
Aí tanto faz, a fórmula que você preferir você usa porque são iguais.
De forma geral, dizemos que é da ordem de , e aproximamos:
Embora eu vá usar isso o tempo todo, isso não é bem verdade. A magnitude dos valores vai estar correta, mas o valor exato não.
Então eu vou te mandar a real, e você vai ter que se decidir dependendo do que seu professor achar melhor.
Na verdade, não é necessariamente próximo de . A fórmula pra ele é:
Ou, rearranjando:
O que, bem, não vejo muita razão pra ser . Muitos lugares ignoram esse e fazem como eu fiz antes, fingindo que ele não existe e só calculando , mas eu não posso te garantir que a sua aula vá ser um desses.
Então o ideal é ver como o professor faz, e confirmar qual das duas formas ele vai usar.
Pra muitos, o que mais importa é o conceito do tunelamento, e não sua fórmula exata.
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ, Física 4, Prova 2, 2012.1
Um feixe com , todos com energia e o número de onda , deslocam-se no sentido positivo do eixo e incidem numa barreira de potencial.
Foi observado que voltaram (sentido negativo do eixo );.
Com base nestas informações podemos afirmar que a probabilidade de um elétron penetrar uma barreira de potencial é de:
- e a energia total de cada elétron é menor que
- e a energia total de cada elétron é maior que
- e a energia total de cada elétron é menor que
- e a energia total de cada elétron é maior que
- e a energia total de cada elétron é menor que
- e a energia total de cada elétron é maior que
- e a energia total de cada elétron é menor que
- e a energia total de cada elétron é maior que
Passo 1
Se de elétrons foram refletidos, elétrons penetraram na barreira.
Logo, a probabilidade de um elétron penetrar na barreira é
Para que um elétron necessariamente penetre na barreira, é necessário que sua energia total seja menor que a energia potencial .
Assim, a opção que melhor se encaixa é a letra (c).
Resposta
Letra (c): e a energia total de cada elétron é menor que
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 211-66, modificado
- Um feixe de prótons de incide em uma barreira de energia potencial de de altura e de largura, a uma taxa correspondente a uma corrente de .
- Quanto tempo é preciso esperar se o feixe contém elétrons em vez de prótons?
Quanto tempo é preciso esperar (em média) para que um próton atravesse a barreira?
Dado:
Massa do elétron
Massa do próton
Passo 1
Letra a)
Primeiro vamos calcular quantos fótons em média incidem na barreira até um finalmente atravessá-la.
O coeficiente de transmissão da barreira é:
Onde
Para calcular :
O que nos dá com :
O coeficiente de transmissão fica:
Ou seja, a cada prótons, em média atravessam a barreira.
Passo 2
A taxa de prótons incidente corresponde a uma que seja tal que criaria uma corrente de .
Como próton tem uma carga de , para gerar uma corrente de são necessários:
Essa é a taxa de prótons que incidem na barreira. A taxa de prótons que atravessa a barreira será:
Seja o tempo que é necessário esperar, em média, para que próton atravesse a barreira. Neste caso, temos:
Passo 3
Letra b)
Se o feixe contém elétrons invés de prótons, teremos:
O coeficiente de transmissão será:
Como os elétrons possuem mesma carga que os prótons, a taxa de elétrons que incide na barreira será equivalente à de prótons. A taxa de elétrons que atravessa a barreira vai ser:
E o tempo médio de espera para que elétron atravesse é:
Resposta
Letra a)
Letra b)
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 212-68, modificado
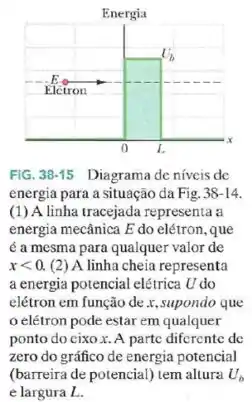
Considere uma barreira de energia potencial como a da Fig.38-15 cuja altura é e cuja largura é .
Qual é a energia de elétrons incidentes para os quais o coeficiente de transmissão é ?
Dado:
Massa do elétron
Passo 1
Primeiro vamos montar o problema.
O coeficiente de transmissão é dado por:
Onde
Queremos achar a energia dos elétrons.
Aplicando logaritmo neperiano:
Agora abrindo o termo à esquerda:
O que fizemos em toda essa sopa de letrinhas foi pegar as equações para a transmissão e explicitar a energia do elétron. Agora, nós só precisamos substituir os valores de cada letra.
Passo 2
Temos:
Substituindo os valores da sopa de letrinhas:
Resposta
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 212-69, modificado
Prótons de incidem em uma barreira de energia potencial de de espessura e de altura. Determine:
- O coeficiente de transmissão T.
- A energia cinética dos prótons que atravessam a barreira por efeito túnel.
- A energia cinética dos prótons que são refletidos pela barreira.
Dêuterons (partículas com a mesma carga que o próton e uma massa duas vezes maior) de incidem na mesma barreira.
Determine os valores de:
Para esse caso.
Dado:
Massa do próton
A conversão de femtometro pra metro é
Passo 1
Letra a)
O coeficiente de transmissão é dado por:
Onde
Temos:
Substituindo em :
Como ficamos com:
Passo 2
Letra b e Letra c)
A energia é conservada tanto na transmissão do próton quanto na sua reflexão.
Como o próton incidente tem uma energia de com uma energia potencial , toda sua energia é cinética.
Como a energia é conservada, o próton que atravessa a barreira terá a mesma energia total, de novo com energia potencial zero.
Assim como o próton que é refletido pela barreira.
Passo 3
Letra d)
O dêuteron tem duas vezes a massa do próton mas com mesma energia. Isso irá alterar apenas o valor de .
Substituindo no coeficiente de transmissão:
Passo 4
Letra e) e Letra f)
Novamente, a energia mecânica do dêuteron é conservada.
Assim, a energia total do dêuteron transmitido e do dêuteron refletido será igual a energia do incidente:
Como em ambos os casos a energia potencial é zero, então a energia total corresponde à energia cinética.
Resposta
Letra a)
Letra b)
Letra c)
Letra d)
Letra e)
Letra f)