Exercícios de Degrau e Tunelamento - Lista de Exercícios Resolvida

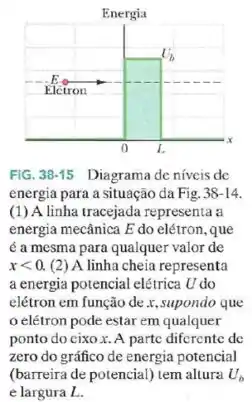
Considere uma barreira de energia potencial como a da Fig.38-15 cuja altura é e cuja largura é .

Qual é a energia de elétrons incidentes para os quais o coeficiente de transmissão é ?

Dado:

Massa do elétron

Prótons de incidem em uma barreira de energia potencial de de espessura e de altura. Determine:

1. O coeficiente de transmissão T.
2. A energia cinética dos prótons que atravessam a barreira por efeito túnel.
3. A energia cinética dos prótons que são refletidos pela barreira.

Dêuterons (partículas com a mesma carga que o próton e uma massa duas vezes maior) de incidem na mesma barreira.

Determine os valores de:

Para esse caso.

Dado:

Massa do próton

A conversão de femtometro pra metro é

1. Um feixe de prótons de incide em uma barreira de energia potencial de de altura e de largura, a uma taxa correspondente a uma corrente de .

Quanto tempo é preciso esperar (em média) para que um próton atravesse a barreira?

2. Quanto tempo é preciso esperar se o feixe contém elétrons em vez de prótons?

Dado:

Massa do elétron

Massa do próton

Um feixe com , todos com energia e o número de onda , deslocam-se no sentido positivo do eixo e incidem numa barreira de potencial.

Foi observado que voltaram (sentido negativo do eixo );.

Com base nestas informações podemos afirmar que a probabilidade de um elétron penetrar uma barreira de potencial é de:

1. e a energia total de cada elétron é menor que
2. e a energia total de cada elétron é maior que
3. e a energia total de cada elétron é menor que
4. e a energia total de cada elétron é maior que
5. e a energia total de cada elétron é menor que
6. e a energia total de cada elétron é maior que
7. e a energia total de cada elétron é menor que
8. e a energia total de cada elétron é maior que

Uma partícula de massa m que se move em uma dimensão possui energia potencial que

varia com a posição como mostra a figura.

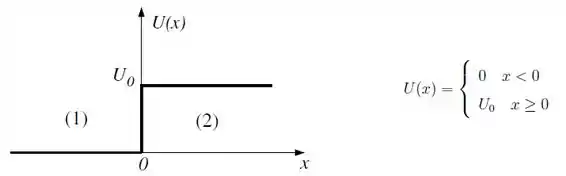
A partícula está em um estado estacionário com energia E φ 1 x   e

da equação de Schrödinger correspondente aos intervalos x ≥ 0

(região 2) respectivamente, são

onde A, B, C e D são constantes arbitrárias.

(a) Determine D. justifique.

(b) Calcule e em função de m, E, U0 e ћ.

(c) Para A = 1, determine B e C.

Um feixe com , todos com energia e o número de onda , deslocam-se no sentido positivo do eixo e incidem numa barreira de potencial.

Foi observado que voltaram (sentido negativo do eixo );.

Com base nestas informações podemos afirmar que a probabilidade de um elétron penetrar uma barreira de potencial é de:

1. e a energia total de cada elétron é menor que
2. e a energia total de cada elétron é maior que
3. e a energia total de cada elétron é menor que
4. e a energia total de cada elétron é maior que
5. e a energia total de cada elétron é menor que
6. e a energia total de cada elétron é maior que
7. e a energia total de cada elétron é menor que
8. e a energia total de cada elétron é maior que

Uma partícula de massa e energia constante move-se sobre o eixo na presença de um degrau de potencial.

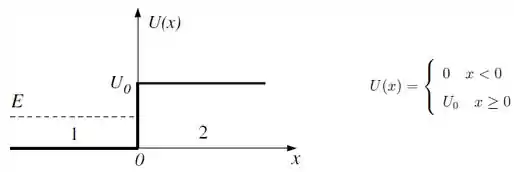
1. Escreva as soluções gerais e da equação de Schrödinger nas regiões () e ().
2. Escreva as condições de contorno que e devem satisfazer.
3. Determine e a menos de uma única constante multiplicativa.