Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Partícula na Caixa – 2D e 3D

Ver Todos os Exercícios

Teoria

A caixa 2D e 3D

Podemos prender o elétron também em um plano ou literalmente numa caixa retangular.

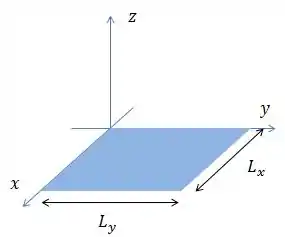
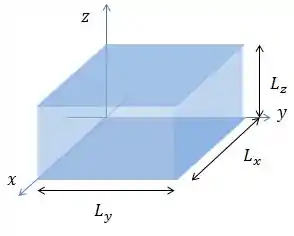
Às vezes você pode ver a armadilha bidimensional ser chamada de “Curral quântico”.

Nestes casos, a função de onda não vai depender apenas de x , mas também de y e z .

A equação de Schrödinger independente do tempo bidimensional e tridimensional dentro da armadilha será:

- ℏ 2 2 m ∂ 2 ψ x , y ∂ x 2 + ∂ 2 ψ x , y ∂ y 2 = E   ψ x , y

- ℏ 2 2 m ∂ 2 ψ x , y , z ∂ x 2 + ∂ 2 ψ x , y , z ∂ y 2 + ∂ 2 ψ x , y , z ∂ z 2 = E   ψ x , y ,   z

Vamos considerar soluções onde dá pra separar cada dependência.

ψ x , y , z = X x Y y Z ( z )

Isso vai fazer com que tenhamos um problema equivalente ao da caixa unidimensional em cada eixo.

As funções de onda serão:

X x = 2 L x sen ⁡ n x π x L x ;     Y y = 2 L y sen ⁡ n y π y L y ;     Z z = 2 L z sen ⁡ n z π z L z

2 D →     ψ x , y = 2 L x ∙ 2 L y sen ⁡ n x π x L x sen ⁡ n y π y L y

3 D →     ψ x , y , z = 2 L x ∙ 2 L y ∙ 2 L z sen ⁡ n x π x L x sen ⁡ n y π y L y sen ⁡ n z π z L z

As energias serão:

E x = n x 2 ∙ h 2 8 m L x 2 ;     E y = n y 2 ∙ h 2 8 m L y 2 ;     E z = n z 2 ∙ h 2 8 m L z 2

2 D →     E x , y = E x + E y = h 2 8 m n x 2 L x 2 + n y 2 L y 2

3 D →     E x , y , z = E x + E y + E z = h 2 8 m n x 2 L x 2 + n y 2 L y 2 + n z 2 L z 2

E em ambos os casos:

n x = 1 ,   2 ,   …

n y = 1 ,   2 ,   …

n z = 1,2 ,   …

Para esse problema aparece um fenômeno novo chamado “degenerescência”.

Imagine que a caixa tridimensional seja um cubo: L x = L y = L z = L . A energia será:

E = h 2 8 m L 2 n x 2 + n y 2 + n z 2

Os estados n x , n y , n z = 1,1 , 2 ; 1,2 , 1 ; 2,1 , 1 vão ter todos a mesma energia!

Isso é a degenerescência: Quando estados diferentes possuem a mesma energia.

Isso pode ocorrer de diferentes maneiras e em diferentes casos. Não é necessário que as dimensões do curral ou da caixa sejam iguais. Então sempre que você for ver transições entre estados energéticos, tome cuidado com isso!

Duas transições completamente diferentes podem ter a mesma diferença de energia.

Por isso é sempre importante tomar cuidado na hora que você for resolver problemas em mais de uma dimensão: Cada energia pode corresponder a várias combinações dos números quânticos envolvidos.

Outra forma de ampliar esse problema seria pensando em várias partículas numa caixa tridimensional. Neste caso, nós recobramos a lei dos gases ideais.

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 242-22

Um elétron é confinado no curral retangular da Fig.39-13, cujas larguras são L x = 800   p m e L y = 1600   p m .

Qual é a energia do estado fundamental do elétron?

Dado:

Massa do elétron m e = 9,109 ∙ 10 - 31   k g

Passo 1

A energia do elétron confinado em um curral retangular é a soma das energias se o elétron estivesse confinado em um poço de potencial infinito no eixo x e no eixo y . Logo:

E n x , n y = h 2 8 m L x 2 n x 2 + h 2 8 m L y 2 n y 2 = h 2 8 m n x 2 L x 2 + n y 2 L y 2

No estado fundamental temos n x = n y = 1 . Logo:

E 1,1 = h 2 8 m 1 L x 2 + 1 L y 2

Passo 2

Do enunciado temos:

Constante de Planck h = 6,626 ∙ 10 - 34   J ∙ s

Massa do elétron m e = 9,109 ∙ 10 - 31   k g

Dimensões do curral L x = 800   p m = 8 ∙ 10 - 10   m e L y = 1600   p m = 16 ∙ 10 - 10   m

E 1,1 = 6,626 ∙ 10 - 34 2 8 ∙ 9,109 ∙ 10 - 31 ∙ 1 8 ∙ 10 - 10 2 + 1 16 ∙ 10 - 10 2

E 1,1 ≅ 6,02479 ∙ 10 - 38 ∙ 0,015625 ∙ 10 20 + 0,00390625 ∙ 10 20

E 1,1 ≅ 1,177 ∙ 10 - 19   J

Em elétrons-volt:

1   e V = 1,602 ∙ 10 - 19   J

E 1,1 ≅ 0,735   e V

Resposta

E 1,1 ≅ 1,177 ∙ 10 - 19   J ≅ 0,735   e V

Exercício Resolvido #2

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 242-23

Um elétron é confinado na caixa retangular da Fig.39-14, cujas dimensões são L x = 800   p m , L y = 1600   p m e L z = 390   p m .

Qual é a energia do estado fundamental do elétron?

Passo 1

A energia do elétron confinado em uma caixa tridimensional é a soma das energias se o elétron estivesse confinado em um poço de potencial infinito no eixo x , no eixo y e no eixo z . Logo:

E n x , n y , n z = h 2 8 m L x 2 n x 2 + h 2 8 m L y 2 n y 2 + h 2 8 m L z 2 n z 2 = h 2 8 m n x 2 L x 2 + n y 2 L y 2 + n z 2 L z 2

No estado fundamental temos n x = n y = n z = 1 . Logo:

E 1,1 , 1 = h 2 8 m 1 L x 2 + 1 L y 2 + 1 L z 2

Passo 2

Do enunciado temos:

Constante de Planck h = 6,626 ∙ 10 - 34   J ∙ s

Massa do elétron m e = 9,109 ∙ 10 - 31   k g

Dimensões da caixa L x = 800   p m = 8 ∙ 10 - 10   m , L y = 1600   p m = 16 ∙ 10 - 10   m e L z = 390   p m = 3,9 ∙ 10 - 10   m

E 1,1 , 1 = 6,626 ∙ 10 - 34 2 8 ∙ 9,109 ∙ 10 - 31 ∙ 1 8 ∙ 10 - 10 2 + 1 16 ∙ 10 - 10 2 + 1 3,9 ∙ 10 - 10 2

E 1,1 , 1 ≅ 6,02479 ∙ 10 - 38 ∙ 0,015625 ∙ 10 20 + 0,00390625 ∙ 10 20 + 0,065746 ∙ 10 20

E 1,1 , 1 ≅ 5 , 1 38 ∙ 10 - 19   J

Em elétrons-volt:

1   e V = 1,602 ∙ 10 - 19   J

E 1,1 , 1 ≅ 3 , 207   e V

Resposta

E 1,1 , 1 ≅ 5,138 ∙ 10 - 19   J ≅ 3,207   e V

Exercício Resolvido #3

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 242-25, modificado

Um elétron (cuja massa é m ) está confinado em um curral retangular de dimensões L x = L e L y = 2 L .

  1. Quantas frequências diferentes o elétron é capaz de emitir ou absorver ao sofrer uma transição entre dois níveis que estão entre os cinco de menor energia?

    2. Que múltiplo de h / 8 m L 2 corresponde:

  2. À menor frequência?
  3. À segunda menor frequência?
  4. À terceira menor frequência?
  5. À maior frequência?
  6. À segunda maior frequência?
  7. À terceira maior frequência?

Passo 1

Letra a)

Quando o elétron sai de um nível de energia E i para um nível de energia E f de menor energia, ele emite um fóton cuja energia é dada por:

E i - E f = h f

Onde f é a frequência do fóton. Isso significa que para cada Δ E corresponde uma única frequência, e vice versa.

Se a transição entre os níveis A e B e entre os níveis C e D forem tais que:

E A - E B = E C - E D

Então ambos emitem luz com a mesma frequência.

Passo 2

A energia de um dado nível do elétron em um curral retangular é dada por:

E n x , n y = h 2 8 m L x 2 n x 2 + h 2 8 m L y 2 n y 2 = h 2 8 m n x 2 L x 2 + n y 2 L y 2

Considerando que L y = 2 L x = 2 L , temos:

E n x , n y = h 2 8 m L 2 n x 2 + n y 2 4

E podemos avaliar quais são os cinco níveis de menor energia.

Como n y 2 está dividido por 4 vemos que o crescimento n y corresponde a menores crescimentos da energia do que o crescimento de n x . Assim, os cinco níveis correspondem a:

n x , n y = 1,1 ; 1,2 ; 1,3 ; 1,4 ; 2,1

Cujas energias em múltiplos de h 2 / 8 m L 2 são:

E 1,1 = 1 2 + 1 2 4 = 1,25

E 1,2 = 1 2 + 2 2 4 = 2

E 1,3 = 1 2 + 3 2 4 = 3,25

E 1,4 = 1 2 + 4 2 4 = 5

E 2,1 = 2 2 + 1 2 4 = 4,25

Eles foram achados por tentativa e erro. Se tentássemos ( 1,5 ) pra cima, teríamos valores para energia, em múltiplos de h 2 / 8 m L 2 , muito grandes:

1 2 + 5 2 4 = 7,25

O mesmo vale para 2,3 para cima:

2 2 + 3 2 4 = 6,25

Por fim, vale um comentário sobre o estado 2,2 . Este estado tem a mesma energia que o estado ( 1,4 ) :

2 2 + 2 2 4 = 5 = 1 2 + 4 2 4

Assim ele também corresponde a um dos níveis de menor energia.

Passo 3

Cada frequência possível corresponde a uma transição de um nível de maior energia para um nível de menor energia.

As transições possíveis são:

1,4 → 2,1 ;   1,4 → 1,3 ;   1,4 → 1,2 ;   1,4 → 1,1

2,1 → 1,3 ;   2,1 → 1,2 ;   2,1 → 1,1

1,3 → 1,2 ;   1,3 → 1,1

1,2 → 1,1

Que são 10 transições no total. Contudo, algumas transições correspondem a um mesmo Δ E , emitindo luz em uma mesma frequência. A variação de energia de todas as transições é (tudo em múltiplos de h 2 / 8 m L 2 ):

Δ E 1,4 → 2,1 = 0,75 ;   Δ E 1,4 → 1,3 = 1,75 ;   Δ E 1,4 → 1,2 = 3 ;   Δ E 1,4 → 1,1 = 3,75

Δ E 2,1 → 1,3 = 1 ;   Δ E 2,1 → 1,2 = 2,25 ;   Δ E 2,1 → 1,1 = 3

Δ E 1,3 → 1,2 = 1,25 ;   Δ E 1,3 → 1,1 = 2

Δ E 1,2 → 1,1 = 0,75

Temos então apenas 8 frequências possíveis correspondentes a:

Δ E = 0,75 ;   Δ E = 1 ; Δ E = 1,25 ; Δ E = 1,75 ; Δ E = 2 ; Δ E = 2,25 ; Δ E = 3 ; Δ E = 3,75

Passo 4

Letra b)

Da discussão anterior, temos que:

f = Δ E h

Ou seja, quanto menor a variação de energia, menor a frequência emitida.

A menor variação de energia possível corresponde às transições 1,2 → 1,1 e 1,4 → 2,1 , sendo a frequência igual a:

f = h 2 8 m L 2 ∙ 0,75 h = h 8 m L 2 ∙ 0,75

Ou seja, f = 0,75   u em múltiplos de h / 8 m L 2 ( u é a unidade correspondente).

Passo 5

Letra c)

A segunda menor variação de energia corresponde a 2,1 → 1,3 :

f = h 2 8 m L 2 ∙ 1 h = h 8 m L 2

Temos f = 1   u em múltiplos de h / 8 m L 2 ( u é a unidade correspondente).

Passo 6

Letra d)

A terceira menor variação de energia corresponde a 1,3 → 1,2 :

f = h 2 8 m L 2 ∙ 1,25 h = h 8 m L 2 ∙ 1,25

Temos f = 1,25   u em múltiplos de h / 8 m L 2 ( u é a unidade correspondente).

Passo 7

Letra e)

A maior variação de energia corresponde a 1,4 → 1,1 :

f = h 2 8 m L 2 ∙ 3,75 h = h 8 m L 2 ∙ 3,75

Temos f = 3,75   u em múltiplos de h / 8 m L 2 ( u é a unidade correspondente).

Passo 8

Letra f)

A segunda maior variação de energia corresponde a   1,4 → 1,2 e 2,1 → 1,1 :

f = h 2 8 m L 2 ∙ 3 h = h 8 m L 2 ∙ 3

Temos f = 3   u em múltiplos de h / 8 m L 2 ( u é a unidade correspondente).

Passo 9

Letra g)

A terceira maior variação de energia corresponde a 2,1 → 1,2 :

f = h 2 8 m L 2 ∙ 2,25 h = h 8 m L 2 ∙ 2,25

Temos f = 2,25   u em múltiplos de h / 8 m L 2 ( u é a unidade correspondente).

Resposta

Letra a)

O elétron é capaz de emitir ou absorver 8 frequências possíveis.

Letra b)

f = 0,75   u

Letra c)

f = 1   u

Letra d)

f = 1,25   u

Letra e)

f = 3,75   u

Letra f)

f = 3   u

Letra g)

f = 2,25   u

Exercício Resolvido #4

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 242-27, modificado

Um elétron (cuja massa é m ) está confinado em uma caixa cúbica de dimensões L x = L y = L z = L .

  1. Quantas frequências diferentes o elétron é capaz de emitir ou absorver ao sofrer uma transição entre dois níveis que estão entre os cinco de menor energia?

    2. Que múltiplo de h / 8 m L 2 corresponde:

  2. À menor frequência?
  3. À segunda menor frequência?
  4. À terceira menor frequência?
  5. À maior frequência?
  6. À segunda maior frequência?
  7. À terceira maior frequência?

Passo 1

Letra a)

Quando o elétron sai de um nível de energia E i para um nível de energia E f de menor energia, ele emite um fóton cuja energia é dada por:

E i - E f = h f

Onde f é a frequência do fóton. Isso significa que para cada Δ E corresponde uma única frequência, e vice versa.

Se a transição entre os níveis A e B e entre os níveis C e D forem tais que:

E A - E B = E C - E D

Então ambos emitem luz com a mesma frequência.

Passo 2

A energia de um dado nível do elétron em uma caixa cúbica é dada por:

E n x , n y , n z = h 2 8 m L x 2 n x 2 + h 2 8 m L y 2 n y 2 + h 2 8 m L z 2 n z 2 = h 2 8 m n x 2 L x 2 + n y 2 L y 2 + n z 2 L z 2

Considerando que L z = L y = L x = L , temos:

E n x , n y , n z = h 2 8 m L 2 n x 2 + n y 2 + n z 2

E podemos avaliar quais são os cinco níveis de menor energia.

Esses cinco níveis correspondem a:

n x , n y ,   n z = 1,1 , 1 ; 1,1 , 2 ; 1,2 , 2 ; 1,1 , 3 ; ( 2,2 , 2 )

Cujas energias em múltiplos de h 2 / 8 m L 2 são:

E 1,1 , 1 = 1 2 + 1 2 + 1 2 = 3

E 1,1 , 2 = 1 2 + 1 2 + 2 2 = 6

E 1,2 , 2 = 1 2 + 2 2 + 2 2 = 9

E 1,1 , 3 = 1 2 + 1 2 + 3 2 = 11

E 2,2 , 2 = 2 2 + 2 2 + 2 2 = 12

Todos estes estados foram encontrados por tentativa e erro, mas avaliar todos os estados com mesma energia que eles é muito trabalhoso. Assim, se você verificar que algum estado tem uma dessas energias acima, este estado será equivalente aos que usamos.

Passo 3

Cada frequência possível corresponde a uma transição de um nível de maior energia para um nível de menor energia.

As transições possíveis são:

1 : 2,2 , 2 → 1,1 , 3 ;   2 : 2,2 , 2 → 1 , 2,2 ;   3 : 2,2 , 2 → 1,1 , 2 ;   4 : 2,2 , 2 → 1,1 , 1

5 : 1,1 , 3 → 1 , 2,2 ;   6 : 1,1 , 3 → 1,1 , 2 ;   7 : 1,1 , 3 → 1,1 , 1

9 : 1 , 2,2 → 1,1 , 2 ;   8 : 1,2 , 2 → 1,1 , 1

10 : 1 , 1 , 2 → 1,1 , 1

Que são 10 transições no total. Contudo, algumas transições correspondem a um mesmo Δ E , emitindo luz em uma mesma frequência. A variação de energia de todas as transições é (tudo em múltiplos de h 2 / 8 m L 2 ):

Δ E 1 = 1 ;   Δ E 2 = 3 ;   Δ E 3 = 6 ;   Δ E 4 = 9

Δ E 5 = 2 ;   Δ E 6 = 5 ;   Δ E 7 = 8

Δ E 8 = 3 ;   Δ E 9 = 6

Δ E 10 = 3

Onde numeramos as transições anteriores de 1 a 10 da esquerda para a direita e de cima para baixo.

Temos então apenas 7 frequências possíveis correspondentes a:

Δ E = 1 ;   Δ E = 2 ; Δ E = 3 ; Δ E = 5 ; Δ E = 6 ; Δ E = 8 ; Δ E = 9

Passo 4

Letra b)

Da discussão anterior, temos que:

f = Δ E h

Ou seja, quanto menor a variação de energia, menor a frequência emitida.

A menor variação de energia possível corresponde à transição 1 , sendo a frequência igual a:

f = h 2 8 m L 2 ∙ 1 h = h 8 m L 2

Ou seja, f = 1   u em múltiplos de h / 8 m L 2 ( u é a unidade correspondente).

Passo 5

Letra c)

A segunda menor variação de energia corresponde à transição 5 :

f = h 2 8 m L 2 ∙ 2 h = h 8 m L 2 ∙ 2

Temos f = 2   u em múltiplos de h / 8 m L 2 ( u é a unidade correspondente).

Passo 6

Letra d)

A terceira menor variação de energia corresponde às transições 2 , 8 e 10 :

f = h 2 8 m L 2 ∙ 3 h = h 8 m L 2 ∙ 3

Temos f = 3   u em múltiplos de h / 8 m L 2 ( u é a unidade correspondente).

Passo 7

Letra e)

A maior variação de energia corresponde à transição 4:

f = h 2 8 m L 2 ∙ 9 h = h 8 m L 2 ∙ 9

Temos f = 9   u em múltiplos de h / 8 m L 2 ( u é a unidade correspondente).

Passo 8

Letra f)

A segunda maior variação de energia corresponde à transição 7:

f = h 2 8 m L 2 ∙ 8 h = h 8 m L 2 ∙ 8

Temos f = 8   u em múltiplos de h / 8 m L 2 ( u é a unidade correspondente).

Passo 9

Letra g)

A terceira maior variação de energia corresponde às transições 3 e 9:

f = h 2 8 m L 2 ∙ 6 h = h 8 m L 2 ∙ 6

Temos f = 6   u em múltiplos de h / 8 m L 2 ( u é a unidade correspondente).

Resposta

Letra a)

O elétron é capaz de emitir ou absorver 7 frequências possíveis.

Letra b)

f = 1   u

Letra c)

f = 2   u

Letra d)

f = 3   u

Letra e)

f = 9   u

Letra f)

f = 8   u

Letra g)

f = 6   u

Exercício Resolvido #5

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 9ª ed. Rio de Janeiro: LTC, 2012, pp 235-30

Um elétron se encontra no estado fundamental de um poço de potencial bidimensional infinito na forma de um quadrado de lado L . Uma sonda quadrada com área de 400 p m 2 é instalada com o centro no ponto     x = L / 8   , y = L / 8 . A probabilidade que o elétron seja detectado é 0,0450. Qual é o valor de L ?

Passo 1

O enunciado dá pra gente a probabilidade então usaremos essa equação:

p x , y = ψ n x , n y x , y 2 d x d y

Onde a função de onda ψ n x , n y x , y é dada pelo produto das funções de cada dimensão:

ψ n x , n y x , y = ψ n x x ψ n y y = 2 L x . 2 L y . s e n n x π . x L x . s e n n y π . y L y

E

p x , y = 4 L x L y . s e n n x π . x L x . s e n n y π . y L y 2 d x d y

p x , y = 4 L x L y . s e n 2 n x π . x L x . s e n 2 n y π . y L y d x d y

Passo 2

Como poço é quadrado L x = L y = L , assim:

p x , y = 4 L 2 . s e n 2 n x π . x L . s e n 2 n y π . y L d x d y

Substituindo a área da sonda por d x d y temos:

p x , y = 4 L 2 . s e n 2 n x π . x L . s e n 2 n y π . y L . 400 p m 2

O elétron está no estado fundamental e com isso n x = 1   e n y = 1 , assim:

p x , y = 4 L 2 . s e n 2 π . x L . s e n 2 π . y L . 400 p m 2

Agora vamos substituir a posição da sonda ( L / 8 ; L 8 ) na função de probabilidade e teremos apenas o L de incógita, assim:

p x , y = 4 L 2 . s e n 2 π L . L 8 . s e n 2 π L . L 8 . 400 p m 2

Arrumando melhor a equação fica:

p x , y = 4 L 2 . s e n 4 π 8 . . 400 p m 2

Passo 3

Precisamos isolar o L e substituir o valor da probabilidade na equação. Isolando o L a equação vai ficar assim:

L = 4 p x , y . s e n 4 π 8 . . 400 p m 2

Com p x , y = 0,0450 , resolvemos a equação e aí:

L = 27,6 p m

Resposta

L = 27,6 p m

Exercício Resolvido #6

Elaboração própria

Num curral dimensional onde L x = 2 L y , a energia no estado fundamental do elétron é de E = 2 × 10 - 20 J , encontre as duas dimensões do curral e calcule o valor da função de onda correspondente para as posicões ( L y , L x ) .

Dado:

Massa do elétron m e = 9,109 × 10 - 31 K g

Passo 1

Como temos apenas duas dimensões podemos calcular a nossa energia dependente apenas de x   e   y .

E x = n x 2 . h 2 8 m L x 2

E y = n y 2 . h 2 8 m L y 2

A energia total é a soma das duas energias então:

E x + E y = E t

n x 2 . h 2 8 m L x 2 + n y 2 . h 2 8 m L y 2 = E t

O enunciado diz que o elétron está no estado fundamental e portanto:

n x = n y = 1

h 2 ( 1 8 m L x 2 + 1 8 m L y 2 ) = E t

Passo 2

Agora que isolamos a energia total podemos trabalhar a equação para encontrarmos os lados da caixa, assim:

h 2 8 m ( L y 2 L x 2 L y 2 + L x 2 L x 2 L y 2 ) = E t

Nosso objetivo é encontrar os lados então devemos isolar as dimensões, assim:

L y 2 + L x 2 L x 2 L y 2 = E t h 2 . 8 m

E como L x = 2 L y , temos:

L y 2 + 2 L y 2 2 L y 2 . L y 2 = E t h 2 . 8 m

L y 2 + 4 L y 2 4 L y 2 . L y 2 = E t h 2 . 8 m

5 L y 2 4 L y 2 . L y 2 = E t h 2 . 8 m

5 4 L y 2 = E t h 2 . 8 m

Rearrumando tudo enfim temos:

5 . h 2 32 . E t . m = L y 2

h . 5 32 . E t . m = L y

Substituindo os valores temos:

L y = 6,626 × 10 - 34 . 5 32 × 2 × 10 - 20 × 9,109 × 10 - 31  

L y = 1,94 n m = 1940 p m

L x = 2 L y = 3,88 n m = 3880 p m

Passo 3

Encontrados os lados podemos encontrar a nossa função de onda, lembrando que para um curral bidimensional a função de onda pode ser descrita por:

ψ x , y = 2 L x . 2 L y . s e n n x π . x L x . s e n n y π . y L y

Substituindo na função o ponto ( L y , L x ) temos:

ψ x , y = 2 L x . 2 L y . s e n n x π . L y L x . s e n n y π . L x L y

Fazendo L x = 2 L y e substituindo n x = n y = 1   temos:

ψ x , y = 2 L y 2 . s e n π . L y 2 L y . s e n π . 2 L y L y

Analisando os argumentos dos senos temos o produto de s e n π 2 × s e n ( 2 π )

E s e n ( 2 π ) = 0 que multiplica toda a função , portanto a função de onda será zero nesse ponto.

ψ x , y = 0

Resposta

L y = 1,94 n m = 1940 p m

L x = 2 l y = 3,88 n m = 3880 p m

ψ x , y = 0

Exercício Resolvido #7

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 9ª ed. Rio de Janeiro: LTC, 2012, pp 235-25

O curral bidimensional infinito da fig. 39-30 tem a forma de um quadrado de lado L = 150 n m . Um detector quadrado, com 5,00 n m de lado e lados paralelos aos eixos x e y, é instalado no centro do ponto ( 0,200 L ; 0,800 L ) . Qual a probabilidade que seja detectado um elétron que está no estado de energia E 1 _ 3 ?

Fig. 39-30.

Passo 1

Como o enunciado pede a probabilidade de encontrarmos um elétron em um determinado

estado vamos usar a equação da probabilidade.

p x , y = ψ n x , n y x , y 2 d x d y

Onde a função de onda ψ n x , n y x , y é dada pelo produto das funções de cada dimensão:

ψ n x , n y x , y = ψ n x x ψ n y y = 2 L x . 2 L y . s e n n x π . x L x . s e n n y π . y L y

E

p x , y = 4 L x L y . s e n n x π . x L x . s e n n y π . y L y 2 d x d y

p x , y = 4 L x L y . s e n 2 n x π . x L x . s e n 2 n y π . y L y d x d y

Passo 2

Como o detector tem dimensões quadradas de 5,00 n m de lado, vamos substituir d x e d y pelas dimensões e considerar que a densidade de probabilidade é constante nos pontos em torno do ponto dado:

p x , y = 4 L x L y . s e n 2 n x π . x L x . s e n 2 n y π . y L y 5,00 . 5,00 p m 2

E como o curral tem forma quadrada L = L x = L y = 150 n m substituímos na equação e fica:

p x , y = 4 × ( 5 p m ) 2   ( 150 p m ) 2 . s e n 2 n x π . x L x . s e n 2 n y π . y L y

A questão pede a energia no nível n x = 1   e n y = 3 assim:

p x , y = 4 × ( 5 p m ) 2   ( 150 p m ) 2 . s e n 2 π . x L x . s e n 2 3 π . y L y

Passo 3

Agora nos resta substituir a posição dada, arrumar e resolver a equação. Temos L x = L y = L e a posição dada no enunciado é ( 0,200 L ; 0,800 L ) , com isso a equação fica:

p x , y = 4 × ( 5 p m ) 2   ( 150 p m ) 2 . s e n 2 π 0,200 L L . s e n 2 3 π 0,800 L L

p x , y = 4 × ( 5 p m ) 2   ( 150 p m ) 2 . s e n 2 0,200 π . s e n 2 2,4 π

Resolvendo temos:

p x , y = 1,4 × 10 - 3

Resposta

p x , y = 1,4 × 10 - 3

Exercício Resolvido #8

Elaboração própria

Numa caixa dimensional onde L x = 4 L y = 2 L z   ,   a função de onda na posição L z , L y 2 ,   L y

é L y × 10 24 , calcule as dimensões da caixa e a energia do elétron considerando que o mesmo está no estado fundamental.

Dado:

Massa do elétron m e = 9,109 × 10 - 31 K g

Passo 1

Precisamos encontrar os lados e nos foi dada a relação entre eles e também o valor da função de onda no ponto assim usaremos essa equação:

ψ x , y = 2 L x . 2 L y . 2 L z . s e n n x π . x L x . s e n n y π . y L y . s e n n y π . z L z

Substituindo na função o ponto L z , L y 2 ,   L y   e também os valores n x = n y = n z = 1 temos:

ψ x , y = 2 L x . 2 L y . 2 L z . s e n π . L z L x . s e n π . L y 2 L y . s e n π . L y L z

Fazendo L x = 4 L y e L z = 2 L y   temos:

ψ x , y = 8 8 . L y 3 . s e n π . 2 L y 4 L y . s e n π . L y 2 L y . s e n π . L y 2 L y

Com o outro lado da equação temos:

L y × 10 24 ,   = 1 L y 3 . s e n π 2 . s e n π 2 . s e n π 2

Como s e n π 2 = 1   :

L y × 10 24 = 1 L y 3

Elevando os dois lados ao quadrado temos:

L y 2 × 10 48 = 1 L y 3

Rearrumando:

L y 5 = 1 10 48

L y = 10 - 48 1 5

L y = 251,2 p m

L x = 4 L y = 1004,8 p m

L z = 2 L y = 502,4 p m

Passo 2

Com três dimensões a energia vai depender de x , y   e z , assim:

E x = n x 2 . h 2 8 m L x 2

E y = n y 2 . h 2 8 m L y 2

E z = n z 2 . h 2 8 m L z 2

A energia total é a soma das energias então:

E x + E y + E z = E t

n x 2 . h 2 8 m L x 2 + n y 2 . h 2 8 m L y 2 + n z 2 . h 2 8 m L z 2 = E t

O enunciado diz que o elétron está no estado fundamental e portanto:

n x = n y = n z = 1

h 2 8 m L x 2 + h 2 8 m L y 2 + h 2 8 m L z 2 = E t

Colocando os termos em evidência temos:

h 2 8 m 1 L x 2 + 1 L y 2 + 1 L z 2 = E t

6,626 × 10 - 34 2 8 × 9,109 × 10 - 31 × 1 1004,8 2 + 1 251,2 2 + 1 502,4 2 × 1 10 - 24 = E t

E t = 1,253 × 10 - 18 J

Resposta

L y = 251,2 p m

L x = 1004,8 p m

L z = 502,4 p m

E t = 1,253 × 10 - 18 J

Exercícios de Livros Relacionados

Um elétron (cuja massa é m ) está confinado em um curral retangular de dimensões L x = L e L y = 2 L . (a) Quantas frequências diferentes o elétron e capaz de emitir ou absorver ao sofrer uma transiçã
Um elétron (cuja massa é m ) está confinado em uma caixa cúbica de dimensões L x = L y = L z (a) Quantas frequências diferentes o elétron é capaz de emitir ou absorver ao sofrer uma transição entre do
Um curral retangular de dimensões L x = L e L y = 2 L contém um elétron. Determine em múltiplos de h 2 / 8 m L 2 , onde m é a massa do elétron, (a) a energia do estado fundamental do elétron; (b) a en
07. Um feixe de elétrons de 2e V incide sobre uma barreira de potencial retangular de 4e V de altura e 10Å Å de espessura. Qual é a probabilidade de transmissão? Qual seria para elétrons de 3e V ?