Relatividade do Tempo
Produzido por Bruno SoaresTeoria
Beleza, vamos começar a colocar os conceitos que já vimos em prática, ok?
Imagine que, no interior de um vagão de trem, existe uma fonte de luz no chão e um espelho no teto.
Vamos nomear dois eventos.
O primeiro evento é a emissão da luz para cima pela fonte, e o segundo evento é o retorno da luz para a fonte, após refletir no espelho.
Vamos analisar esse cenário a partir de dois referenciais.
Primeiro Referencial
O primeiro referencial, que vamos chamar de , se move com a mesma velocidade do vagão. Portanto, ele está parado em relação ao vagão.
Nele, o Homer vai medir o intervalo de tempo entre os dois eventos.
Homer verá a luz percorrer a trajetória conforme a figura abaixo.
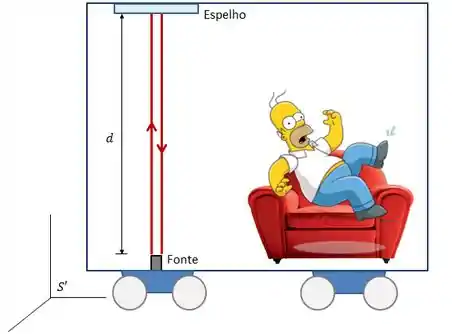
O tempo que o Homer mede entre os dois eventos é dado por:
Onde é a altura do vagão e é a velocidade da luz.
Segundo Referencial
O segundo referencial, que vamos chamar de , está parado e vendo o vagão se mover com velocidade . Portanto, ele está em movimento em relação ao referencial .
Nele, a Lisa vai medir o intervalo de tempo entre os dois eventos.
Para Lisa, a luz vai realizar uma trajetória diferente.
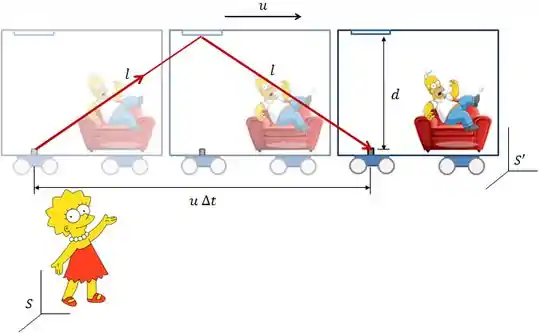
O tempo que a Lisa mede entre os dois eventos é dado por:
Onde, usando o teorema de Pitágoras:
Portanto:
Dilatação do Tempo
Para relacionar com , vou isolar nas duas equações o e vamos ver no que dá.
Do tempo medido por Homer, temos:
Do tempo medido por Lisa, temos:
Igualando essas duas expressões, vamos ter o seguinte:
Organizando essa equação, vamos chegar no seguinte:
Por fim:
Essa equação mostra que há uma diferença entre o tempo medido pelo Homer (referencial ) e pela Lisa (referencial ).
Como a velocidade do vagão é, e deve ser sempre, menor do que a velocidade da luz , a equação nos mostra que, para os mesmos eventos, o tempo medido pelo Homer , que está se movendo junto com o vagão, é menor do que o tempo medido pela Lisa , no referencial que está em repouso.
Portanto, quanto maior a velocidade entre os referenciais, maior será o intervalo de tempo medido por Lisa .
Ah! Também podemos escrever a equação da seguinte forma:
Onde é chamado de Fator de Lorentz, e é dado por:
Obs.: Em alguns lugares, a razão pode ser substituída pelo parâmetro de velocidade .
Distância Percorrida
E se ele nos perguntar sobre a distância percorrida nesse intervalo?
Simples!
Bom, a distância percorrida pelo trem de acordo com o nosso referencial ( – Lisa) será dada por:
De acordo com o nosso referencial, o tempo será:
Logo, a distância percorrida pelo trem que mediremos será:
Então, é importante saber exatamente distinguir os referenciais e saber em qual deles estamos trabalhando.
Parece mole, mas é importante ficar esperto, ok?
Segundo Referencial
Dilatação do Tempo
Distância Percorrida
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ-P2-2011.2-ME01
Os tripulantes da USS Enterprise NCC-1701, que se encontra a uma distância de da Terra, enviam uma mensagem para o centro de controle da Terra, avisando que irão cessar as comunicações durante , intervalo de tempo durante o qual o software da nave será atualizado.
Supondo que a Enterprise viaja a uma velocidade de em relação à Terra, quantos dias terão transcorrido na Terra nesse período?
- Nenhuma das anteriores
Passo 1
Trata-se de um problema de Dilatação do tempo, cuja equação é dada por:
Onde é o tempo próprio, no caso, o tempo medido na nave. E é a velocidade da nave.
Passo 2
Onde:
;
;
Logo:
Resposta
Letra (i):
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 177.
Uma partícula instável de alta energia entra em um detector e deixa um rastro com de comprimento viajando a uma velocidade de , antes de decair.
Qual é o tempo de vida próprio da partícula? Em outras palavras, quanto tempo a partícula levaria para decair se estivesse em repouso em relação ao detector?
Passo 1
O intervalo de tempo medido no referencial em repouso é dado por:
Passo 2
Utilizando a equação de dilatação do tempo, podemos determinar o tempo próprio:
Substituindo os valores, teremos:
Resposta
Exercício Resolvido #3
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, cap 37, pp 172 - 37.7.
Uma espaçonave se afasta da Terra com velocidade de em relação à Terra e a seguir volta com a mesma velocidade.
A espaçonave transporta um relógio atômico que foi cuidadosamente sincronizado com outro relógio que permaneceu na Terra.
A espaçonave retorna a seu ponto de partida dias (um ano) mais tarde, conforme medido pelo relógio que ficou na Terra.
Qual a diferença entre os intervalos de tempo, em horas, medidos pelos dois relógios?
Qual dos dois relógios, o que ficou na Terra ou o da espaçonave, indica o menor intervalo de tempo?
Passo 1
Trata-se de um problema de Dilatação do tempo, cuja equação é dada por
Onde é o tempo medido na nave, é o tempo medido na Terra e é a velocidade da nave.
O problema nos pede inicialmente a diferença entre os intervalos de tempo, em horas, medidos pelos dois relógios.
Passo 2
Onde:
;
;
;
Logo:
Passo 3
Passo 4
Qual dos dois relógios, o que ficou na Terra ou o da espaçonave, indica o menor intervalo de tempo?
O relógio na espaçonave indicará o menor tempo.
Resposta
;
Relógio na espaçonave;
Exercício Resolvido #4
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, cap 37, pp 172 – 37.5.
O píon negativo é uma partícula instável que possui vida média aproximadamente igual a (medida no sistema de referência do píon).
- Quando o píon se desloca com velocidade muito grande em relação ao laboratório, sua vida média em relação ao laboratório é de . Calcule a velocidade do píon expressa como uma fração de .
- Qual é a distância que o píon percorre no laboratório durante sua vida média?
Passo 1
a) Quando o píon se desloca com velocidade muito grande em relação ao laboratório, sua vida média em relação ao laboratório é de . Calcule a velocidade do píon expressa como uma fração de .
O problema nos diz que o tempo medido no referencial (em movimento) do píon é , e nos diz também que o tempo medido no laboratório (em repouso) é .
Assim, podemos usar a equação de Dilatação do tempo, dada por:
Passo 2
;
;
Logo:
Passo 3
b) Qual é a distância que o píon percorre no laboratório durante sua vida média?
Como estamos medindo a distância no referencial do laboratório, o tempo medido para vida média é .
Assim:
Onde:
;
;
;
Logo:
Resposta
a)
b)
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 178.
Um astronauta parte da Terra e viaja com velocidade de em direção à estrela Vega, que está a de distância. Quanto tempo terá passado, de acordo com os relógios da Terra, quando o astronauta chegar a Vega; quando os observadores terrestres receberem a notícia de que o astronauta chegou a Vega? Qual é a diferença entre o tempo de viagem de acordo com os relógios da Terra e o tempo de viagem de acordo com o relógio de bordo?
Passo 1
Quanto tempo terá passado, de acordo com os relógios da Terra, quando o astronauta chegar a Vega?
Bom, como os dois eventos (saída e chegada do astronauta à Vega) ocorrem no mesmo lugar, visto da nave, o tempo medido na nave é o nosso tempo próprio. Beleza? Esse tempo pode ser calculado por:
Podemos escrever a velocidade da luz em anos-luz/ano. Basta lembrar que a luz viaja 1 ano-luz em 1 ano, ou seja, . Assim:
Passo 2
Além disso, sabemos que o tempo próprio se relaciona com o tempo medido de outro referencial por:
Portanto, o tempo na Terra será:
Passo 3
Quanto tempo terá passado, de acordo com os relógios da Terra, quando os observadores terrestres receberem a notícia de que o astronauta chegou a Vega?
O tempo total será igual à soma do tempo levado pelo astronauta para chegar à estrela com o tempo levado para o sinal chegar à Terra.
Se o sinal viaja na velocidade da luz e a estrela está à de distância, o sinal levará para chegar na Terra, logo:
Passo 4
Qual é a diferença entre o tempo de viagem de acordo com os relógios da Terra e o tempo de viagem de acordo com o relógio de bordo?
O tempo de viagem de acordo com os relógios da Terra foi o que calculamos no item , logo:
E o tempo de viagem de acordo com a nave, que é o tempo próprio, foi calculado na também:
Com isso, a diferença de tempo será:
Resposta
Exercício Resolvido #6
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 183.
Um píon é criado na parte superior da atmosfera da Terra quando um raio cósmico colide com um núcleo atômico. O píon assim formado desce em direção à superfície da Terra com uma velocidade de .
Em um referencial no qual estão em repouso os píons decaem com uma vida média de . No referencial da Terra, que distância um píon percorre (em média) na atmosfera antes de decair?
Passo 1
A distância medida no referencial da Terra será:
Utilizando a equação de dilatação do tempo, temos que:
Logo:
Passo 2
Substituindo a expressão do fator de Lorentz, temos:
Onde:
Finalmente: