Contração do Comprimento
Teoria
A situação que vamos criar agora é bem parecida com a que vimos anteriormente.
Imagine o mesmo vagão que usamos no capítulo de Dilatação do Tempo e que, em seu interior, agora existe uma régua, colocada horizontalmente.
Em uma das extremidades da nossa régua está uma fonte de luz e na outra está um espelho. Então, agora o feixe de luz que vamos observar se move horizontalmente.
O primeiro evento é a emissão da luz para a direita pela fonte, e o segundo evento é o retorno da luz para a fonte, após refletir no espelho.
Vamos analisar esse cenário de dois referenciais.
Primeiro Referencial
Novamente, o primeiro referencial, que vamos chamar de , se move com a mesma velocidade do vagão. Nele, o Homer vai observar a trajetória do feixe de luz entre os dois eventos.
Homer verá a luz percorrer a trajetória conforme a figura abaixo.
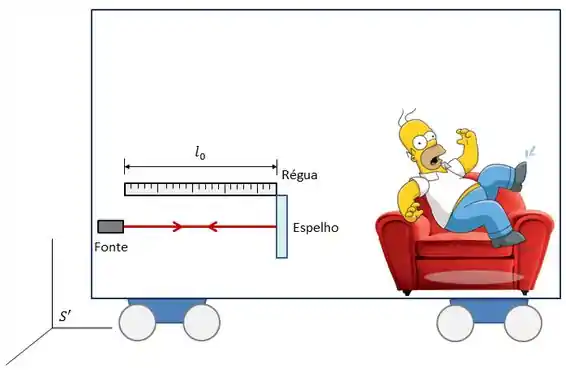
Já que a luz vai e volta, o Homer vai ver a luz percorrendo uma distância . Logo:
Onde é o comprimento da régua observado pelo Homer.
Segundo Referencial
O segundo referencial, que vamos chamar de , está parado e vendo o vagão se mover com velocidade . Portanto, ele está em movimento em relação ao referencial .
Nele, a Lisa vai observar a trajetória do feixe de luz entre os dois eventos.
Para Lisa, a luz vai realizar uma trajetória diferente.
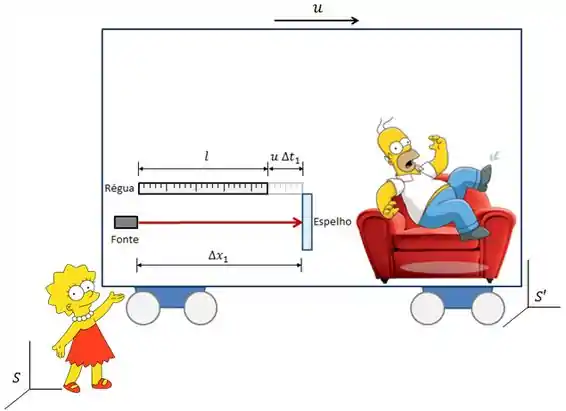
A régua se desloca com velocidade no referencial da Lisa. Vamos dividir a análise em duas partes.
Quando a luz sai da fonte, até encontrar o espelho, ela percorre uma distância , dada por:
Quando a luz reflete no espelho, até voltar para a fonte, ela percorre uma distância , dada por:
Onde é o comprimento da régua observado pela Lisa.
O tempo total é dado por:
Contração do Comprimento
Podemos relacionar e pela equação de Dilatação do tempo que vimos antes, ela é essa aqui:
Agora que, para a nossa nova situação, já achamos expressões para e , o nosso trabalho agora é substituir as expressões que encontramos na equação acima.
Enfim, organizando isso tudo, a equação que encontramos é essa:
O termo é recorrentemente chamado de “comprimento próprio” ou “comprimento de repouso”, que é o comprimento medido por Homer no referencial , onde os dois eventos ocorrem no mesmo local do espaço (a saída do laser da fonte e a chegada do laser na fonte).
Essa equação mostra que há uma diferença entre o comprimento da régua observado por Homer (referencial ) e por Lisa (referencial ).
Como a velocidade do vagão é menor do que a velocidade da luz , a equação nos mostra que, para os mesmos eventos, o comprimento medido pelo Homer , que está se movendo junto com o vagão, é maior do que o comprimento medido pela Lisa , no referencial que está em repouso.
Portanto, quanto maior a velocidade entre os referenciais, menor será o comprimento medido por Lisa .
Ah! Também podemos escrever a equação assim:
Onde é chamado de Fator de Lorentz, e é dado por:
Vamos parar por aqui, por enquanto, e fazer alguns exercícios pra fixar melhor tudo isso.
Contração do Comprimento e o Tempo
Imagina que, malandramente, você está na sua nave inocente, a explosão de uma estrela te surpreende e você sai correndo de lá. A sua nave possui velocidade e você calcula que, pra escapar, terá que percorrer (medida no referencial das estrelas).
A primeira questão é a seguinte: Quanto tempo, medido no referencial das estrelas, será necessário para você fugir de lá?
Bom, o tempo medido no próprio referencial das estrelas será dado por:
Até aqui nenhum problema já que todos os dados e cálculos estão sendo feitos para o mesmo referencial.
A próxima questão é a seguinte: Quanto tempo, medido no seu referencial, será necessário para fugir de lá?
Se liga que tem dois jeitos de calcular esse intervalo de tempo .
O primeiro jeito é: calculado o intervalo no referencial das estrelas, você pode usar a equação de dilatação do tempo para calcular , se liga:
O segundo jeito é: se você ainda não calculou o intervalor , podemos partir da seguinte equação de cinemática.
Usando a equação de contração dos comprimentos, temos que:
Substituindo esse cara na equação acima, teremos:
No final das contas, os dois jeitos dão no mesmo lugar (como tem que ser), mas é importante saber exatamente distinguir os referenciais e saber em qual deles estamos trabalhando.
Para não vacilar, vamos fazer alguns exercícios pra fixar melhor isso.
Segundo Referencial
Contração do Comprimento
Contração do Comprimento e o Tempo
Exercícios Resolvidos
Exercício Resolvido #1
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, cap 37, pp 172 – 37.9.
Uma espaçonave da Federação de Comércio passa sobre o planeta Coruscant com velocidade de .
Uma cientista na superfície de Coruscant mede o comprimento dessa espaçonave e obtém um valor igual a .
A seguir, a espaçonave pousa na superfície de Coruscant, e a mesma cientista mede o comprimento essa espaçonave, que agora está em repouso. Qual e o valor que ela encontra?
Passo 1
Trata-se de um problema de Contração dos comprimentos, cuja equação é dada por:
Onde é o comprimento medido no referencial em repouso (no caso, medido quando a nave pousa), é o comprimento medido no referencial em movimento (no caso, medido quando a nave está em movimento) e é a velocidade da nave.
Passo 2
Onde:
;
;
Logo:
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 183.
O raio da Terra é e a velocidade orbital do planeta é . Suponha que a Terra passe por um observador com essa velocidade. Qual é a redução do diâmetro da Terra na direção do movimento, do ponto de vista do observador?
Passo 1
A redução do diâmetro da Terra será dada por:
Onde é dado pela equação da contração de comprimento:
Passo 2
Logo:
Substituindo a expressão do fator de Lorentz, teremos:
Onde:
Portanto:
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4, 8º ed. Rio de Janeiro: LTC , 2008, pp 177-11.
Uma espaçonave cujo comprimento de repouso é passa por uma base espacial a uma velocidade de .
Qual é o comprimento da nave no referencial da base?
Qual é o intervalo de tempo registrado pelos tripulantes da base entre a passagem da proa e a passagem da popa da espaçonave?
Passo 1
Qual é o comprimento da nave no referencial da base?
Através da equação de contração do comprimento, temos que:
Onde:
Logo:
Passo 2
Qual é o intervalo de tempo registrado pelos tripulantes da base entre a passagem da proa e a passagem da popa da espaçonave?
O intervalo de tempo registrado pelos tripulantes da base será:
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4, 8º ed. Rio de Janeiro: LTC , 2008, pp 177-8.
Uma régua no referencial faz um ângulo de com o eixo . Se a régua está se movendo paralelamente ao eixo do referencial com velocidade de em relação ao referencial , qual é o comprimento da régua no referencial ?
Obs.: Considere o comprimento de repouso da régua igual a .
Passo 1
Quando a régua se mover, será observada a contração do comprimento apenas na sua componente na direção .
Assim, as componentes serão dadas por:
Passo 2
Quando a régua está se movendo, o comprimento da componente da régua na direção será:
Substituindo os valores, teremos:
Assim, o comprimento medido pelo observador no referencial será:
Onde . Portanto:
Resposta
Exercício Resolvido #5
PUCRIO-P2-2013.2
Uma nave espacial passa por uma base espacial com velocidade , onde é a velocidade da luz no vácuo. O comprimento da pista de pouso medido pelos funcionários da base em terra é .
Calcule o comprimento da pista no referencial do piloto da nave.
Obtenha o intervalo de tempo registrado pelo piloto entre a passagem do início e do final da pista.
Passo 1
Para obter o comprimento da pista no referencial da nave, devemos recorrer à equação para a contração dos comprimentos, ela diz:
Onde é o comprimento da pista no referencial da nave, é o comprimento da pista no referencial da terra e é o denominado fator de Lorentz.
Vamos primeiro determinar :
Passo 2
Voltando à equação da contração dos comprimentos, temos:
Passo 3
O tempo registrado pelo piloto entre a passagem do início até o final da pista, pode ser encontrada pela seguinte fórmula:
Para o piloto, temos:
Resposta
Exercício Resolvido #6
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, cap 37, pp 173 – 37.13.
Em relação a um observador na Terra, a pista de lançamento de uma espaçonave possui comprimento de .
- Qual é o comprimento da pista medido pelo piloto de uma espaçonave que se desloca com velocidade igual a em relação à Terra?
- Uma observadora em repouso na Terra mede o intervalo de tempo desde o momento em que a espaçonave está diretamente sobre o início da pista até o instante em que a espaçonave está diretamente sobre o final da pista. Que resultado ela obtém?
- O piloto da espaçonave mede o intervalo de tempo desde o momento em que espaçonave passa diretamente sobre o início da pista até o instante em que ela passa diretamente sobre o final da pista. Que resultado ele obtém?
Passo 1
a) Qual é o comprimento da pista medido pelo piloto de uma espaçonave que se desloca com velocidade igual a em relação à Terra?
Se estamos falando de comprimento, essa é a fórmula que usaremos:
Passo 2
O problema nos diz que medido no referencial em repouso é , e nos diz também que a velocidade do piloto é .
Do referencial do piloto, é a Terra que está se movendo com velocidade . Assim, estamos interessados em saber o valor de .
Onde:
;
;
;
Logo:
Passo 3
b) Uma observadora em repouso na Terra mede o intervalo de tempo desde o momento em que a espaçonave está diretamente sobre o início da pista até o instante em que a espaçonave está diretamente sobre o final da pista. Que resultado ela obtém?
A observadora na Terra (referencial em repouso) vê a espaçonave se deslocando com a velocidade , assim, o tempo medido por ela é:
;
;
Onde é o comprimento da pista medida por ela.
Portanto:
Passo 4
c) O piloto da espaçonave mede o intervalo de tempo desde o momento em que espaçonave passa diretamente sobre o início da pista até o instante em que ela passa diretamente sobre o final da pista. Que resultado ele obtém?
Já que conhecemos o valor do comprimento da pista medido pelo piloto , usar simplesmente a relação:
Resposta
a)
b)
c)