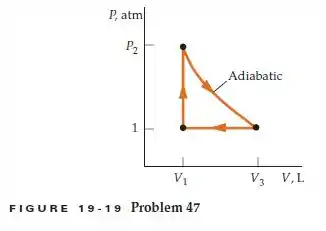
No ciclo mostrado na Figura 19-19, 1,00 mol de um gás diatômico ideal está inicialmente a uma pressão de 1,00 atm e a uma temperatura de 0,0ºC. O gás é aquecido a um volume constante até e é, então, expandido adiabaticamente até que sua pressão seja novamente 1,00 atm. Ele é, depois, comprimido à pressão constante de volta ao seu estado original. Determine:
- A temperatura após a expansão adiabática;
- O calor absorvido ou liberado pelo sistema durante cada etapa;
- A eficiência desse ciclo;
- A eficiência de um ciclo de Carnot operando entre os extremos de temperatura deste ciclo.
Passo 1
Muito bem, na letra a nós queremos saber qual é a temperatura depois da expansão adiabática, ou seja, .
Nós temos duas opções, calcular usando a relação entre o ponto 2 e 3 ou entre o ponto 1 e 3. Qual vamos escolher?
Nós temos mais informações sobre 1, então vamos trabalhar com ele, ok?
Se usarmos a equação para os gases ideais:
Como a pressão é constante:
O termo é constante para ambos os pontos:
Isolando
Deu problema, né? Não temos Então vamos ver o que o ponto 2 nos trás. O processo entre 2 e 3 é adiabático, então vale uma relação
Onde
Aqui g equivale aos graus de liberdade. Como estamos trabalhando com gás diatômico,
Substituindo e isolando o volume:
Lembrando que:
Então:
Ainda não temos , então vamos usar o processo a volume constante de 1 até 2. Usando o mesmo raciocínio que o usado de 1 para 3:
Isolando
Agora sim, sabemos que:
Achando a pressão:
Agora conseguimos achar o volume, lembrando que para um gás ideal nestas condições de temperatura e pressão :
Calma que estamos quase acabando. Agora que sabemos o volume vamos calcular o que queremos:
Ou em graus Celsius:
Bem grande né! Mas ainda não terminamos !
Passo 2
Na letra b precisamos descobrir o calor absorvido ou doado. A equação para o calor à volume constante é dado por:
A capacidade térmica é dada por:
Já sabemos que
No calor:
Substituindo:
O processo de 2 até 3 é adiabático. Então já sabemos o calor:
Para o último processo, o calor deve ser calculado à pressão constante:
A capacidade térmica é dada por:
Já sabemos que
No calor:
Substituindo:
Passo 3
Na letra c, precisamos da eficiência. E para ela também usamos uma fórmula:
Sabemos que:
Para acharmos o trabalho, vamos lembrar da primeira lei da termodinâmica:
Como estamos trabalhando com o ciclo, não há variação da energia interna, já que a temperatura inicial e final são iguais:
Mas vamos com calma. Vamos relacionar o trabalho sobre o gás com o trabalho realizado pelo gás:
Substituímos tudo:
E se fosse um ciclo de Carnot? O que seria diferente? A forma como calculamos a eficiência:
Substituindo: