A barra rígida representanda abaixo sofre um carregamento vertical. Calcule o valor máximo de para que a barra se mantenha estável, sabendo que ambas as molas lineares tem coeficiente e a mola torcional tem coeficiente .
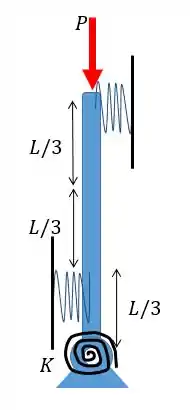
Passo 1
Vamos lá, galera. Esse problema pede o carregamento máximo ou seja ele quer . Para achar a gente precisa considerar duas coisas:
- O sistema está em equilíbrio, portanto, podemos utilizar as equações de equilíbrio.
- O equilíbrio é estável logo as variações angulares são pequenas, desta forma podemos fazer as aproximações para ângulos pequenos.
Portanto a primeira coisa que devemos fazer é um diagrama das foças. Partiu?
Passo 2
Fazendo o diagrama das forças considerando uma pequena deflexão vamos ter:
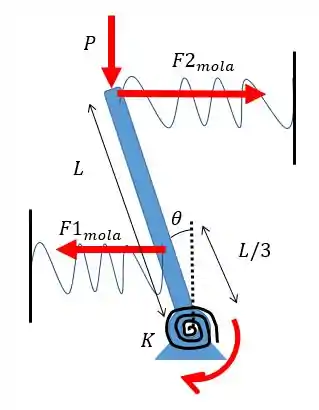
Agora fica mais fácil de comparar essas forças, correto?
Como a gente não sabe o valor da força que atua no pino. Nós vamos aplicar o somatório de momentos nesse ponto:
Agora vamos ter que os momentos e agem no sentido contrário aos de e da mola torcional, portanto:
obs: O momento de uma mola torcional é dado por
Vamos calcular a força das molas no próximo passo.
Passo 3
A força de cada mola será dada por:
Substituindo na equação vamos obter:
Lembrando que podemos fazer a aproximação porque o ângulo é pequeno. Assim vamos ter:
Simplificando pelo termo vamos ter:
Como a variação angular é pequena para mantermos o equilíbrio estável a gente pode considerar , logo: