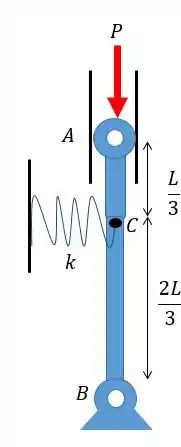
Duas barras rígidas e são conectadas a uma mola de constante , como mostrado. Sabendo-se que a mola pode atuar tanto à tração quanto à compressão, determinar a carga crítica para o sistema.
Passo 1
Vamos resolver mais um problema aqui sobre carga crítica num sistema com mola. Para começar é importante fazer um esquema de como fica o nosso sistema com uma pequena angulação:
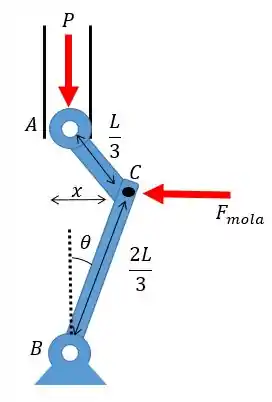
Aí, pessoal, a partir disso a gente tem que aplicar nossas equações de equilíbrio estático e lembrar de fazer as aproximações:
Já que se trata de um ângulo bem pequeno.
Passo 2
Ao olhar o nosso diagrama podemos ver que é a própria deformação da mola. Podemos calcular o valor de por meio dos dois triângulos formados:
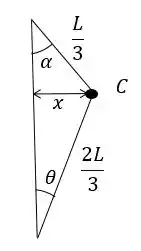
Podemos calcular de duas formas:
Fazendo a aproximação:
Vamos ter:
Logo,
Passo 3
Agora que sabemos os dois ângulos nós podemos voltar ao nosso diagrama e analisar apenas a barra :
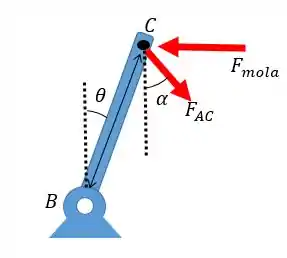
Onde a força é a força que a barra faz na barra , como essa força depende verticalmente apenas da força nós vamos ter:
Logo,
Fazendo o somatório dos momentos em nós vamos ter:
Aplicando as aproximações dos ângulos e nós vamos ter:
Como
E a equação da mola é:
Onde:
Logo,