Sabendo-se que a mola torcional em é de constante e que a barra é rígida, determinar a carga crítica .
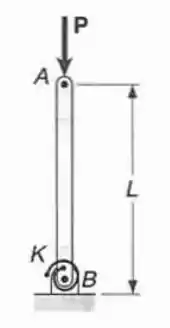
Passo 1
A carga crítica, pedida no problema, é a maior carga que mantenha o sistema numa equilíbrio estável. Ou seja, temos de pensar sempre em duas coisas:
- O sistema está em equilíbrio, portanto, podemos utilizar as equações de equilíbrio.
- O equilíbrio é estável logo as variações angulares são pequenas, desta forma podemos fazer as aproximações para ângulos pequenos.
Passo 2
Para aplicar as equações de equilíbrio vamos fazer um diagrama de forças, já considerando uma pequena angulação.
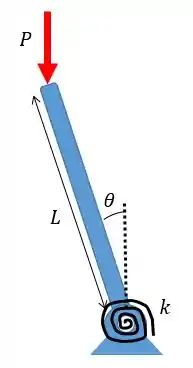
Agora vamos aplicar o somatório de momentos em relação ao pino, lembrando que o sistema está em equilíbrio, logo, esta soma deve ser igual a zero.
Desta forma vamos ter que o momento da carga será igual ao momento da mola de torção:
Fazendo a aproximação para ângulos pequenos podemos obter: