A coluna é composta por um elemente estrutural rígido preso por um pino na base e acoplado a uma mola no topo. Se a mola não estiver esticada quando a coluna estiver em posição vertical, determine a carga crítica que pode ser aplicada à coluna.
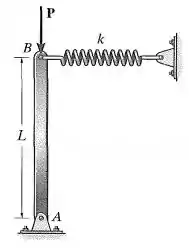
Passo 1
O problema pede a carga crítica que pode ser aplicada à coluna, ou seja, a maior carga que pode ser aplicada à coluna sem que haja alteração no equilíbrio.
Desta forma, a gente tem que fazer um diagrama das forças e achar uma relação entre a força da mola e a carga .
Lembre-se também que iremos considerar ângulos pequenos porque se a angulação for muito grande vamos ter uma situação de equilíbrio não-estável, que não queremos.
Passo 2
Vamos começar fazendo o diagrama de corpo livre dessa barra, considerando uma pequena deformação:
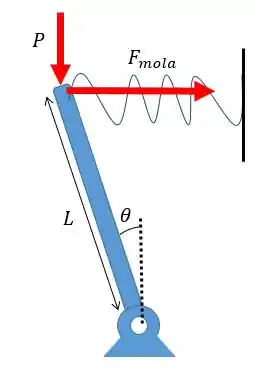
A partir desse diagrama a gente pode aplicar o somatório dos momentos no pino e igualar a zero para obter a condição de equilíbrio:
A deformação da mola é dada por , logo:
Simplificando:
Como o nosso ângulo é muito pequeno podemos fazer a aproximação
Logo,
Passo 3
Resposta
Ei, a resposta está no passo a passo :)