Uma bola de tênis lisa, com massa de e de diâmetro, é golpeada na sua parte superior (topsipin) a , o que lhe confere uma rotação de . Calcule a sustentação aerodinâmica atuando sobre a bola. Avalie o raio de curvatura da sua trajetória na máxima elevação do plano vertical. Comapre com o raio quando não houver rotação.
(Dados: e )
Passo 1
Bom, vamos lá! Esse problema se relaciona com o que chamamos de efeito Magnus. O efeito Magnus ocorre quando um corpo, além de se mover em uma direção, roda em torno de seu próprio eixo. Dá uma olhada aqui em baixo:
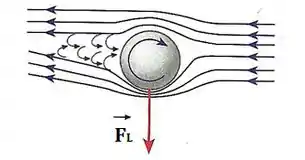
Observe que ao golpearmos a bola de tênis na parte superior, ela apresentará determinada rotação (sentido horário) além de se mover para frente. Então, a gente percebe que:
- Na parte de cima: a velocidade da superfície da bola tem sentido oposto ao escoamento do ar.
- Na parte de baixo: a velocidade da superfície da bola tem mesmo sentido que o escoamento do ar.
Dessa forma, o fluido na parte de cima é desacelerado e o fluido na parte de baixo é acelerado, surgindo, assim, regiões com diferentes velocidades e, consequentemente, regiões com diferentes pressões.
Como a velocidade na parte superior é menor que a velocidade na parte inferior, logo a pressão em cima será maior que a pressão em baixo, gerando uma força de sustentação de cima para baixo ().
Bacana! A gente já viu como calcular a força de sustentação:
A área da projeção () será a área do círculo de diâmetro igual ao da esfera ():
Substituindo os valores de cada grandeza, teremos:
Passo 2
Como vimos, a bola é atingida na parte de cima e “ganha rotação” no sentido horário, resultando numa força resultante para baixo. Usando a segunda lei de Newton para avaliar a curvatura da trajetória no plano vertical temos:
Lembre-se de que a aceleração centrípeta () é dada por:
Substituindo a expressão na equação, teremos:
Então, dividindo a equação por e isolando o raio (), temos que:
Passo 3
Se não houvesse rotação, as linhas de corrente seriam simétricas e a gente não verificaria diferenças de pressão. Logo a componente da força de sustentação () seria zero! Consequentemente a expressão do raio seria dada por:
Concluimos, portanto, que há diferença entre as situações com rotação e sem rotação, logo o efeito Magnus é importante!
Resposta
A força de sustentação calculada foi de:
Os valores do raio calculados na situação com rotação () e sem rotação () são respectivamente: