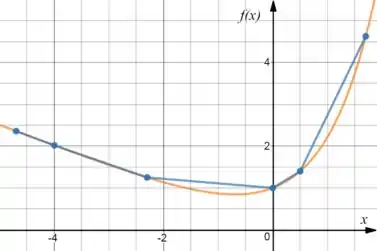
Seja a tabela abaixo gerada pela função , encontre a função spline linear que interpola os pontos tabelados e esboce o gráfico de ambas as funções.
Passo 1
Primeiro definimos:
Passo 2
Agora é só aplicação de fórmulas:
:
:
:
:
:
Passo 3
Juntando tudo temos:
O gráfico vai ficar assim:
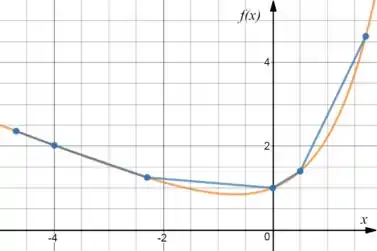
Resposta
Exercícios de Livros Relacionados
Considere a tabela:Ajuste os pontos acima por uma função do tipox l n ( a x + b ) , usando o método dos mínimos quadrados
Considere a tabela:Por qual das funções:a) y t = t a + b t ; b) y = a b t você ajustaria esta tabela?
Usando o método dos mínimos quadrados encontre aeb tais que y=a x b ajusta os dados:
Mr. K. P. Lear (1609, Way of Astronomy) teve a ideia de que a Terra se move ao redor do Sol em órbita elíptica, com o Sol em um dos focos. Depois de muitas observações e cálculos, ele obteve a tabela
Após serem efetuadas medições num gerador de corrente contínua, foram obtidos os seguintes valores indicados por um voltímetro e um amperímetro.Faça um gráfico dos dados.a) Ajuste os dados por polinôm