As tabelas na parte inferior correnspondem as alturas dos aulos matriculados na disciplina PROBEST-2013-2 turma 3VB. Usando os dados apresentados, pede-se:
- Através do diagrama de Pareto, construa o Diagrama de Frequência e o Histograma (Esboçe Gráficos de Frequência e % cumulativo).
- Se a probabilidade de um aluno de PROBEST faltar à aula é de , e supondo que os alunos faltem às aulas de maneira estatisticamente independentes entre si e no tempo, qual a chance de nessa turma o professor não ter nenhum aluno presente em determinado dia de aula?
Passo 1
Essa aparentemente é uma questão bastante simples, que apenas nos pede uma boa leitura do gráfico para montar nosso diagrama de Frequência e % Cumulativo.
Passo 2
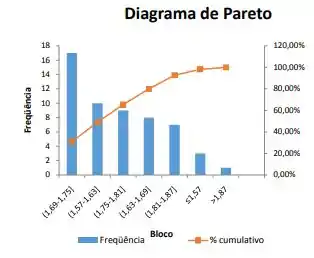
(a) Primeiro vamos olhar para o gráfico e tentar descobrir quantas amostras diferentes nós temos. Pelo histograma, temos e para as alturas respectivamente, que nos da um total de 55.
Agora vamos calcular qual é a probabilidade de cada grupo existir, ou seja
, ,
, , ,
Passo 3
Entretanto queremos escrever em nossa tabela de frequência e % cumulativo o valor em porcentagem cumulativo, ou seja, a probabilidade de existir um aluno de todos os grupos até aquele momento, ou seja
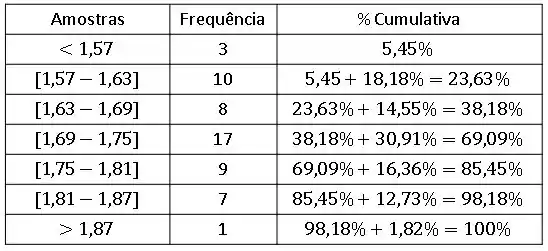
Que é colocada em ordem crescente de altura. Gerando assim uma tabela de Frequência e % Cumulativo
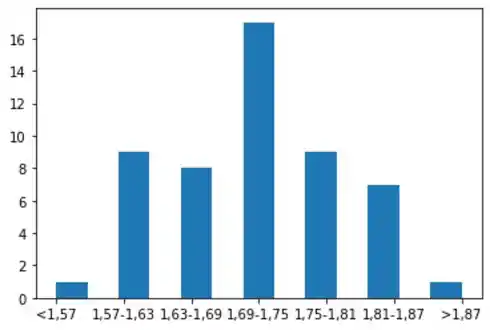
Plotando nosso Histograma, temos
Passo 4
(b) Sabemos que o total de aluno é de , onde os mesmo tem um probabilidade independente em si e no tempo de de faltarem algum dia.
Assim estamos interessados em calcular a que pode ser descrita pela distribuição binomial e é dada por
Na qual é a probabilidade dos alunos faltarem de forma independentes, é o número de aulos, e será nosso numero de alunos faltantes, além de não podermos esquecer que Na qual é uma combinação e vale
Assim podemos aplicar as coisa que já sabemos para calcular , ou seja
Que é um número muito pequeno
Resposta
(b)