3º EE de Física 1 da UFPE - 2013.1

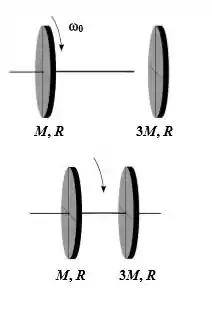
Um disco de massa e raio está girando com uma velocidade angular preso a uma haste que fura o disco através do eixo perpendicular passando pelo seu centro. Um segundo disco com massa três vezes maior que o primeiro e de mesmo raio, inicialmente em repouso, é acoplado à mesma haste de modo que o conjunto passa a girar com uma mesma velocidade angular, como mostra a figura ao lado. Dados: O momento de inércia do disco uniforme em relação ao eixo que passa pelo centro de massa é ; o momento de inércia da haste é desprezível.

(a) Determine a velocidade angular do sistema composto pelos dois discos em termos da velocidade angular .

(b) Que percentagem da energia cinética de rotação inicial é perdida devido à adição do segundo disco? Para determinar a percentagem de energia perdida utilizar a expressão onde e as energias cinéticas inicial e final respectivamente.

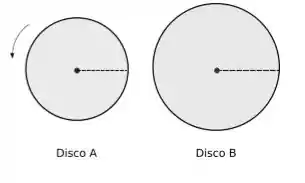
A figura mostra dois discos que podem girar em torno de seus centros independentemente. No instante , as retas de referência dos dois discos têm a mesma orientação (como mostrado no desenho); o disco já está girando com uma velocidade angular constante e o disco parte do repouso com uma aceleração angular constante de.

(a) Em que instante as duas retas de referência têm o mesmo deslocamento angular ?

(b) Qual será o primeiro instante , após , para o qual as duas retas de referência estão paralelas com a linha que une o centro dos dois discos?

(c) Considere agora que o deslocamento angular do disco varia no tempo com , onde está em radianos. Em qual instante a velocidade angular de é igual à velocidade angular de ?

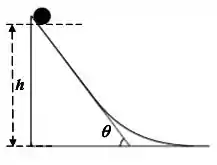
Um disco é liberado a partir do repouso do alto de uma superfície inclinada de altura (medida desde o solo até o ponto mais baixo do disco como mostrado na figura) e rola suavemente sem deslizar até a parte mais baixa da superfície. No primeiro trecho, a superfície é retilínea e forma um ângulo com a horizontal, como mostrado na figura. Dados: o momento de inércia do disco homogêneo com relação a um eixo que passa pelo centro de massa é , onde é a massa do disco e é seu raio. Considere .

(a) Calcule a aceleração do centro de massa do disco quando ele ainda se encontra no trecho retilíneo na superfície.

(b) Determine a velocidade do centro de massa quando o disco atinge a parte mais baixa da trajetória.