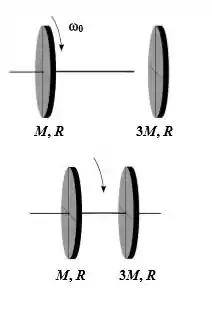
Um disco de massa e raio está girando com uma velocidade angular preso a uma haste que fura o disco através do eixo perpendicular passando pelo seu centro. Um segundo disco com massa três vezes maior que o primeiro e de mesmo raio, inicialmente em repouso, é acoplado à mesma haste de modo que o conjunto passa a girar com uma mesma velocidade angular, como mostra a figura ao lado. Dados: O momento de inércia do disco uniforme em relação ao eixo que passa pelo centro de massa é ; o momento de inércia da haste é desprezível.
(a) Determine a velocidade angular do sistema composto pelos dois discos em termos da velocidade angular .
(b) Que percentagem da energia cinética de rotação inicial é perdida devido à adição do segundo disco? Para determinar a percentagem de energia perdida utilizar a expressão onde e as energias cinéticas inicial e final respectivamente.
Passo 1
(a) Aplicando a conservação do momento angular para os instantes antes e após a adição do segundo disco, temos:
E, portanto, podemos concluir que .
Passo 2
(b) A energia cinética rotacional quando há apenas um disco é:
Já a energia cinética para o caso de dois discos é:
A fração da energia cinética perdida é , ou seja, da energia cinética inicial de rotação é perdida.
Resposta
(a)
(b)