3º EE de Física 1 da UFPE - 2019.2

Uma esfera maciça e homogênea de massa e raio é mantida inicialmente em repouso sobre um plano inclinado de um ângulo (ver Figura 1). Quando liberada, a esfera passa a rolar sem deslizar plano abaixo.

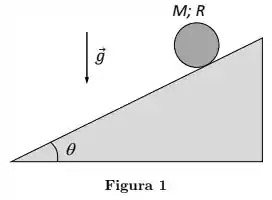
Considere as afirmativas abaixo sobre a situação em que a esfera já está em movimento:

1. A força de atrito é nula.
2. O trabalho da força de atrito é nulo.
3. O torque da força de atrito em relação ao centro de massa da esfera é nulo.

Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).

4. e
5. e
6. e
7. Todas
8. Nenhuma

Um canhão está preso na borda de um carrossel de raio que pode girar sem atrito sobre um eixo vertical fixo que passa pelo seu centro (ver Figura 2). O carrossel e o canhão têm um momento de inércia total em relação a esse eixo. O conjunto encontra-se inicialmente em repouso. O canhão então dispara uma bala de massa com uma velocidade tangencialmente ao carrossel. O conjunto carrossel + canhão passa a girar devido ao disparo.

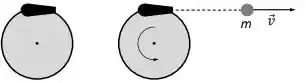
Após o disparo, qual é a velocidade angular do conjunto carrossel + canhão?

Uma partícula de massa descreve uma trajetória na forma de uma circunferência de raio . Sua posição angular (em rad.) e dada pela expressão:

Com o tempo em segundos.

O módulo da aceleração tangencial da partícula (em ) no instante vale:

Um canhão está preso na borda de um carrossel de raio que pode girar sem atrito sobre um eixo vertical fixo que passa pelo seu centro (ver Figura 2). O carrossel e o canhão têm um momento de inércia total em relação a esse eixo. O conjunto encontra-se inicialmente em repouso. O canhão então dispara uma bala de massa com uma velocidade tangencialmente ao carrossel. O conjunto carrossel + canhão passa a girar devido ao disparo.

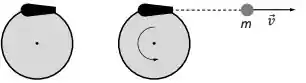
Considere o sistema formado pelo carrossel, canhão e bala. Sejam o momento linear total do sistema, o momento angular total do sistema em relação ao centro do carrossel e a energia mecânica total do sistema. No processo de disparo do canhão, é (são) conservado(s) apenas:

4. e
5. e
6. e
8. Nenhum

Uma partícula de massa descreve uma trajetória na forma de uma circunferência de raio . Sua posição angular (em rad.) e dada pela expressão:

Com o tempo em segundos.

O módulo do momento angular da partícula (em ) em relação ao centro da circunferência no instante vale:

Uma partícula de massa descreve uma trajetória na forma de uma circunferência de raio . Sua posição angular (em rad.) e dada pela expressão:

Com o tempo em segundos.

A energia cinética de rotação da partícula (em joules) no instante vale:

Um motor é ligado a um disco homogêneo de massa e raio (ver Figura 3). Em algumas situações, uma corda ideal enrolada no disco pode ser conectada a um bloco. A corda não desliza sobre o disco. Considere .

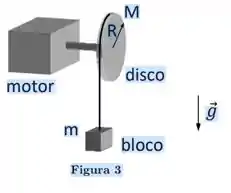
(A) (1,0 ponto) Suponha, inicialmente, a situação em que a corda ainda não esteja conectada ao bloco, ou seja, o bloco ainda não se encontra pendurado na figura ao lado. Nesse caso, a tensão na corda é nula. O motor aplica no disco um torque de módulo , em relação ao seu centro, que o faz girar. Escreva a equação de 2ª lei de Newton para o disco e determine a sua aceleração angular gerada por este torque.

Dado: Momento de inércia de um disco homogêneo de massa e raio em relação a um eixo perpendicular à sua superfície e passando no seu centro: .

(B) (1,5 ponto) Considere, agora, que um bloco de massa foi conectado à corda, como mostra a figura acima. Novamente, o motor aplica um torque , em relação ao centro do disco, que o faz girar, de modo que o bloco sobe verticalmente. Escreva as equações de 2ª lei de Newton para o disco e para o bloco.

(C) (1,5 ponto) Resolva o sistema de equações do item (B) e determine a aceleração angular do disco e a tensão na corda.