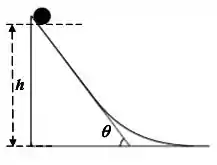
Um disco é liberado a partir do repouso do alto de uma superfície inclinada de altura (medida desde o solo até o ponto mais baixo do disco como mostrado na figura) e rola suavemente sem deslizar até a parte mais baixa da superfície. No primeiro trecho, a superfície é retilínea e forma um ângulo com a horizontal, como mostrado na figura. Dados: o momento de inércia do disco homogêneo com relação a um eixo que passa pelo centro de massa é , onde é a massa do disco e é seu raio. Considere .

(a) Calcule a aceleração do centro de massa do disco quando ele ainda se encontra no trecho retilíneo na superfície.

(b) Determine a velocidade do centro de massa quando o disco atinge a parte mais baixa da trajetória.

Na parte retilínea da superfície, percebemos que o disco está submetido às forças gravitacional (que aponta ao longo do plano para baixo) e a força de atrito estático (que aponta ao longo do plano para cima) pois a forca puxa o disco pelo centro de massa tentando fazer o ponto que toca a rampa deslizar para baixo). O atrito é estático pois o disco rola suavemente de modo que e o ponto que toca a rampa tem velocidade zero.

Portanto, a segunda lei de Newton linear e a segunda lei de Newton angular ficam como mostrado a seguir:

onde o torque horário é positivo (podemos usar essa definição; é uma escolha que não muda a natureza física do problema). Ficamos com:

Portanto, . Com e , temos que .