2º EE de Física 1 da UFPE - 2019.1

Uma partícula de massa m = 2,0 kg move-se ao longo do eixo x sujeita a uma única força F. A dependência de F com a posição x da partícula é mostrada na Figura 1. A energia potencial associada à forçaa F é U. Quando a partícula está em x = 0, ela tem velocidade = 2,0 m/s no sentido positivo do eixo x.

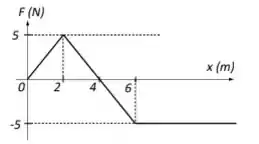
A energia cinética da partícula na posição x = 4,0 m é:

a) 0 J

b) 4 J

c) 10 J

d) 14 J

e) 24 J

f) 25 J

g) 49 J

h) 100 J

i) 144 J

Uma partícula de massa m = 2,0 kg move-se ao longo do eixo x sujeita a uma única força F. A dependência de F com a posição x da partícula é mostrada na Figura 1. A energia potencial associada à forçaa F é U. Quando a partícula estáa em x = 0, ela tem velocidade = 2,0 m/s no sentido positivo do eixo x.

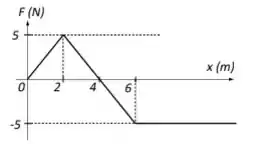
Considere as afirmativas:

I. No intervalo 0 ≤ x ≤ 4,0 m, a velocidade da partícula é máxima em x = 2,0 m.

II. A variação da energia potencial ∆U entre x = 0 e x = 2,0 m é positiva.

III. O trabalho realizado pela força F entre x = 2,0 m e x = 4,0 m é negativo.

Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).

a) I

b) II

c) III

d) I e II

e) I e III

f) II e III

g) Todas

h) Nenhuma

Uma partícula de massa m = 2,0 kg move-se ao longo do eixo x sujeita a uma única força F. A dependência de F com a posição x da partícula é mostrada na Figura 1. A energia potencial associada à forçaa F é U. Quando a partícula está em x = 0, ela tem velocidade = 2,0 m/s no sentido positivo do eixo x.

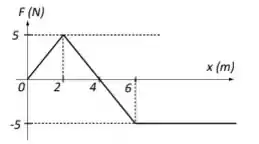
Em qual posição a partícula para momentaneamente antes de retornar?

a) 2,0 m

b) 2,8 m

c) 3,8 m

d) 4,0 m

e) 5,8 m

f) 6,0 m

g) 7,0 m

h) 7,8 m

i) 8,0 m

Duas massas de modelar deslizam sobre uma superfície horizontal de gelo, sem atrito. As massas possuem velocidades iniciais , e colidem de forma que seguem juntas com velocidade , conforme a Figura abaixo.

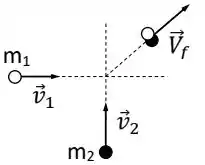
Considere as afirmativas abaixo:

I) A energia mecânica total das massas depois da colisão é a mesma que antes da colisão.

II) O momento linear total das massas depois da colisão é o mesmo que antes da colisão.

III) O momento linear da massa m1 depois da colisão é o mesmo que antes da colisão.

Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).

a) I

b) II

c) III

d) I e II

e) I e III

f) II e III

g) Todas

h) Nenhuma

Duas massas de modelar deslizam sobre uma superfície horizontal de gelo, sem atrito. As massas possuem velocidades iniciais , e colidem de forma que seguem juntas com velocidade , conforme a Figura abaixo.

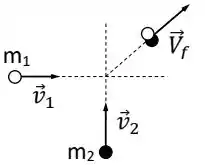
A variação da energia cinética total das massas, , devido a colisão é:

a) 0 J

b) −6,0 J

c) −3,0 J

d) −1,5 J

e) 1,5 J

f) 3,0 J

g) 6,0 J

h) 8,0 J

Duas massas de modelar deslizam sobre uma superfície horizontal de gelo, sem atrito. As massas possuem velocidades iniciais , e colidem de forma que seguem juntas com velocidade , conforme a Figura abaixo.

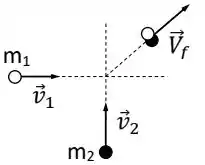
Considere as massas das partículas = 6,0 kg e = 4,0 kg, e suas respectivas velocidades antes da colisão e . A velocidade (em m/s) das partículas após a colisão é:

a)

b)

c)

d)

e)

f)

g)

h)

Na Figura 3, o bloco A de massa = 2,0 kg encontra-se inicialmente em repouso, preso a uma mola ideal comprimida de 0,10 m. A constante el ́astica da mola vale k = 40 N/m. Nos itens a seguir, considere g = e despreze todos os atritos. O bloco não perde o contato com a superfície.

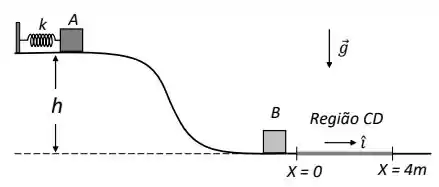
a) Calcule a velocidade do bloco ap ́os descer a rampa de altura h = 0,19 m em relação ao nível do solo.

b) Após descer a rampa, o bloco A sofre uma colisão perfeitamente inelástica com um bloco B de massa = 8,0 kg inicialmente em repouso. A colisão faz um bloco grudar no outro. Calcule a velocidade dos blocos imediatamente após a colisão.

c) Após a colisão, os blocos permanecem grudados e ingressam na região CD horizontal, com início na posição x = 0 e término em x = 4,0 m. Nessa região, os blocos estão sujeitos a força variável (em newtons), que os acelera para a frente, onde x é a posição dos blocos e é o vetor unitrio horizontal para a direita. Calcule o trabalho realizado por F entre as posições x = 0 e x = 4,0 m.

Sugestão: Faça o gráfico de F em função de x.