PF de Física 1 da UFPE - 2015.2

O deslocamento de um corpo é descrito pela equação horária:

Onde o tempo é dado em segundos. O vetor aceleração do corpo é igual a:

(a)

(b)

(c)

(d)

(e)

(f)

A figura mostra um sistema composto por duas partículas, de mesma massa , sobre as quais atuam forças, representadas pelas setas.

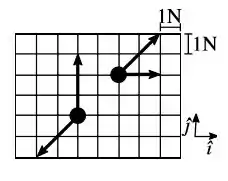
Nesta situação, a aceleração do centro de massa do sistema é igual a:

(a)

(b)

(c)

(d)

(e)

(f)

Uma partícula se desloca ao longo do eixo sujeita à energia potencial mostrada na figura. Sabendo que é um ponto de retorno. Qual é a energia cinética da partícula em ?

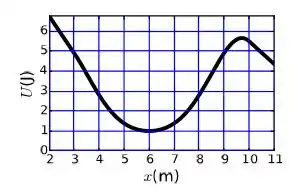
(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

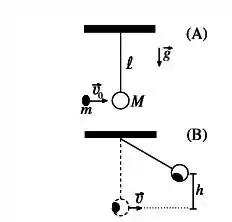
Um corpo de massa encontra-se pendurado na vertical por uma haste de comprimento e massa desprezível. Uma partícula de massa atinge o corpo com velocidade (figura()). Imediatamente após a colisão os dois corpos se deslocam unidos com velocidade . Considere a aceleração gravitacional no local .

(a) Determine .

(b) Após a colisão o sistema se desloca verticalmente de uma altura , quando fica momentaneamente em repouso (figura()). Calcule .

Uma esfera homogênea de massa e raio está conectada sem atrito a um eixo vertical passando no seu centro. A esfera está inicialmente em repouso com um besouro de massa parado na sua linha equatorial. Num dado instante o besouro começa a se mover ao longo da linha equatorial com velocidade de módulo constante .

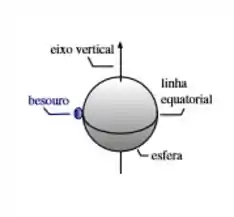
(a) Sabendo que existe atrito entre a esfera e o besouro, o momento angular total do sistema ‘esfera + besouro’ ´e conservado? Justifique.

(b) Calcule o momento de inércia do sistema ‘esfera besouro’ em relação ao eixo mencionado. Dado: Momento de inércia de uma esfera homogênea de massa e raio ao redor de um eixo passando no seu centro: .

(c) Calcule a velocidade angular que a esfera adquire quando o besouro se movimenta.

Um fio inextensível e de massa desprezível conecta dois blocos, de massas e , onde . O fio passa sem deslizar por um roldana que pode girar sem atrito em torno de um eixo que passa pelo ponto . A roldana tem raio e momento de inércia em relação ao ponto . O sistema é liberado em uma região com aceleração gravitacional . Sabe-se que o módulo da aceleração do sistema, , é não nulo. Sejam e os módulos das trações no fio nos trechos e respectivamente.

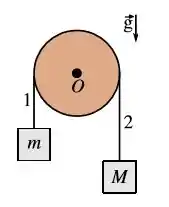
Pode-se afirmar que:

(a)

(b)

(c)

(d)

(e)

(f)