Um fio inextensível e de massa desprezível conecta dois blocos, de massas e , onde . O fio passa sem deslizar por um roldana que pode girar sem atrito em torno de um eixo que passa pelo ponto . A roldana tem raio e momento de inércia em relação ao ponto . O sistema é liberado em uma região com aceleração gravitacional . Sabe-se que o módulo da aceleração do sistema, , é não nulo. Sejam e os módulos das trações no fio nos trechos e respectivamente.
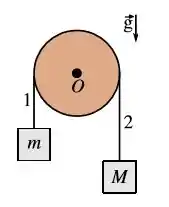
Pode-se afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
Passo 1
Vamos fazer o diagrama de corpo livre de todos os elementos do sistema:
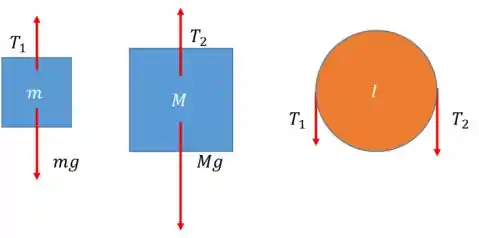
Usando a segunda lei de newton pros blocos e pra polia:
Somando a primeira e a segunda equações:
E também, da terceira equação:
Portanto, analisando as opções, vemos que a resposta é a letra (c)
Resposta
Letra (c)