1º EE de Física 1 da UFPE - 2019.2

O gráfico da Figura mostra a velocidade em função do tempo de duas partículas (A e B) em movimento retilíneo.

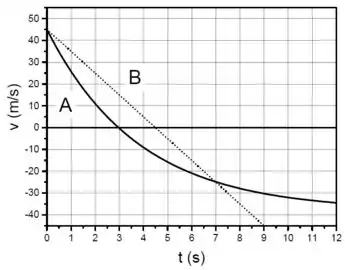
Considere as afirmativas abaixo:

(I) A velocidade inicial (em t = 0) da partícula B é igual à velocidade inicial da partícula A.

(II) A aceleração da partícula A é igual à aceleração da partícula B no instante t = 7 s.

(III) A aceleração média da partícula A entre os instantes t = 0 e t = 7 s é maior que a aceleração média da partícula B entre os mesmos instantes.

Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).

(a) I

(b) II

(c) III

(d) I e II

(e) I e III

(f) II e III

(g) Todas

(h) Nenhuma

O gráfico da Figura mostra a velocidade em função do tempo de duas partículas (A e B) em movimento retilíneo.

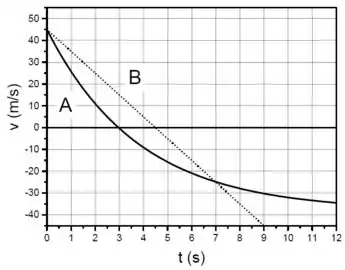
A aceleração média da partícula A entre os instantes e é:

O gráfico da Figura mostra a velocidade em função do tempo de duas partículas (A e B) em movimento retilíneo.

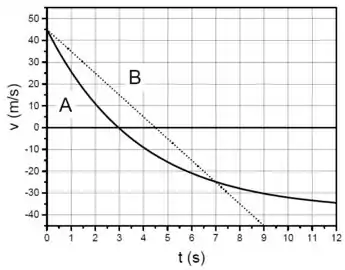
A partícula B inverte o sentido do seu movimento no instante . Nesse caso, pode-se afirmar que a aceleração da partícula B vale:

A posição de uma partícula em metros é descrita pelo vetor:

onde o tempo t é dado em segundos.

Qual é o vetor velocidade média da partícula (em) entre os instantes e ?

que a aceleração da partícula B vale:

A posição de uma partícula em metros é descrita pelo vetor:

onde o tempo t é dado em segundos.

Qual é o vetor velocidade da partícula (em ) no instante ?

Uma partícula executa um movimento circular uniforme (MCU) no plano , com centro na origem e sentido anti-horário. Em certo instante o seu vetor velocidade (em m/s) vale . No instante , o vetor posição da partícula é , onde R é o raio do MCU.

Sabendo que o período do MCU é , qual é a sua aceleração centrípeta (em ) no instante ?

Um bloco de massa encontra-se inicialmente mantido em repouso sobre um plano inclinado de um ângulo , preso a uma das pontas de uma corda ideal (veja a Figura 2). A corda passa por uma polia ideal e tem a sua outra ponta presa a um bloco de massa . Os coeficientes de atrito estático e cinético entre e o plano inclinado são e , respectivamente. Considere , e . Num certo instante, o conjunto dos blocos é liberado.

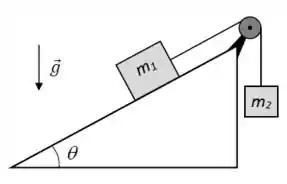
1. Faça o diagrama de corpo livre de cada bloco depois que o conjunto é liberado, desenhando e nomeando todas as forças que atuam sobre eles.
2. Calcule o módulo da força normal que o plano inclinado exerce sobre .
3. Depois de liberado, o conjunto se move? Justifique sua resposta.
4. Calcule o módulo da força de tração na corda.
5. Calcule o módulo da força de atrito e especifique seu sentido.